
如图,直线a,b被直线c所截,a∥b,∠1=∠2,若∠4=70°,则∠3等于( )
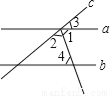
A. 40° B. 50° C. 70° D. 80°
A 【解析】试题分析::∵∠1=∠2,∠3=40°,∴∠1=×(180°-∠3)=×(180°-40°)=70°, ∵a∥b,∴∠4=∠1=70°.故选:C.科目:初中数学 来源:山东省2018届九年级12月月考数学试卷 题型:单选题
如图,AB为⊙O的直径,点C在⊙O上,若∠C=16°,则∠BOC的度数是( )
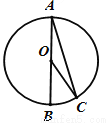
A. 74° B. 48° C. 32° D. 16°
C 【解析】∵OA=OC, ∴∠A=∠C=16°, ∴∠BOC=∠A+∠C=32°. 故选C。查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2016届九年级下学期二模数学试卷 题型:填空题
已知直角坐标内,半径为2的圆心坐标为(3,-4),当该圆向上平移m个单位长度时,若要此圆与x轴没有交点,则m的取值范围是 _______________.
m<2或m>6 【解析】圆心向上平移m个单位长度后坐标为(3,m-4), ∵圆与x轴没有交点, ∴所以圆心到x轴的距离>2, 即m-4>2或m-4<-2, ∴m>6或m<2. 故答案为m>6或m<2.查看答案和解析>>
科目:初中数学 来源:2017年海南省海口市中考数学模拟试卷 题型:解答题
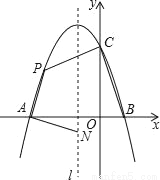
如图,抛物线y=ax2+bx+c与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴l为x=﹣1.
(1)求抛物线的解析式并写出其顶点坐标;
(2)若动点P在第二象限内的抛物线上,动点N在对称轴l上.
①当PA⊥NA,且PA=NA时,求此时点P的坐标;
②当四边形PABC的面积最大时,求四边形PABC面积的最大值及此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源:2017年海南省海口市中考数学模拟试卷 题型:填空题
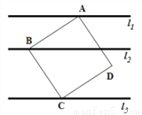
直线l1∥l2∥l3,正方形ABCD的三个顶点A、B、C分别在l1、l2、l3上,l1与l2之间的距离是4,l2与l3之间的距离是5,则正方形有ABCD的面积是___________.
查看答案和解析>>
科目:初中数学 来源:2017年海南省海口市中考数学模拟试卷 题型:单选题
下列说法正确的是( )
A. 任何非负数都有两个平方根 B. 一个正数的平方根仍然是正数
C. 只有正数才有平方根 D. 负数没有平方根
D 【解析】试题解析:A. 非负数0的平方根是0,只有一个,故本选项错误; B. 一个正数有两个平方根,它们互为相反数,故本选项错误; C. 因0的平方根是0,故本选项错误; D. 负数没有平方根,故本选项正确; 故选D.查看答案和解析>>
科目:初中数学 来源:2017年海南省海口市中考数学模拟试卷 题型:单选题
若数轴上的点A、B分别与有理数a、b对应,则下列关系正确的是( )
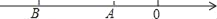
A. a<b B. ﹣a<b C. |a|<|b| D. ﹣a>﹣b
C 【解析】根据数轴的特征∵b查看答案和解析>>
科目:初中数学 来源:2017年海南省中考数学模拟试卷 题型:单选题
下列运算正确的是( )
A. 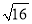 =8 B.
=8 B. 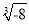 =﹣2 C.
=﹣2 C. 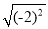 =﹣2 D.
=﹣2 D. 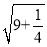 =3+
=3+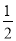
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(八) 题型:填空题
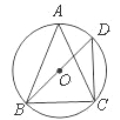
如图,⊙O是等腰三角形ABC的外接圆,AB=AC,∠A=45°,BD为⊙O的直径,BD= ,
,
连结CD,则BC= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com