
线段是轴对称图形,它有 ________条对称轴.
2 【解析】根据轴对称图形的概念,知线段有2条对称轴,即线段所在的直线和线段的垂直平分线.故答案为:2.科目:初中数学 来源:人教版七年级下册数学第6章实数单元检测卷 题型:单选题
下列说法错误的是( )
A. 5是25的算术平方根 B. ±4是64的立方根
C. (﹣4)3的立方根是﹣4 D. (﹣4)2的平方根是±4
B 【解析】A. ∵52=25,∴ 5是25的算术平方根,故正确; B. ∵43=64,∴4是64的立方根,故不正确; C. ∵(﹣4)3=-64,∴(﹣4)3的立方根是﹣4,故正确; D. ∵(﹣4)2=16,∴(﹣4)2的平方根是±4,故正确; 故选B.查看答案和解析>>
科目:初中数学 来源:北师大版九年级下册数学第一章直角三角形的边角关系单元检测卷 题型:填空题
观光塔是潍坊市区的标志性建筑,为测量其高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°.已知楼房高AB约是45m,根据以上观测数据可求观光塔的高CD是 m.
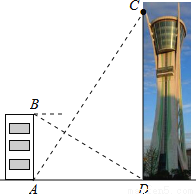
查看答案和解析>>
科目:初中数学 来源:北师大版七年级下册数学 第五章 生活中的轴对称 单元检测卷 题型:解答题
(本题6分) 如图,在11×11的正方形网格中,网格中有一个格点△ABC(即三角形的顶点都在格点上).
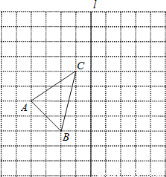
(1)在图中作出△ABC关于直线l对称的△A1B1C1 (要求A与A1,B与B1,C与C1相对应) ;
(2)在直线l上找一点P,使得△PAC的周长最小.
【解析】 试题分析:(1)根据网格结构找出点A、B、C 关于直线l的对称点A1、B1、C1的位置,然后顺次连接即可; (2)有题意知只要让PA+PC最短即可,也就是根据对称的性质,C′A与l的交点即为P点,因此这时候的. △PAC的周长最小.查看答案和解析>>
科目:初中数学 来源:北师大版七年级下册数学 第五章 生活中的轴对称 单元检测卷 题型:填空题
“中”字是一个成轴对称的汉字,它有 ________ 条对称轴.
2 【解析】根据轴对称图形和对称轴的概念可得:中有2条对称轴。 故答案为:2.查看答案和解析>>
科目:初中数学 来源:北师大版七年级下册数学 第五章 生活中的轴对称 单元检测卷 题型:单选题
在平面直角坐标系中,以点A(2,4)为圆心,1为半径作⊙A,以点B(3,5)为圆心,3为半径作⊙B,M、N分别是⊙A,⊙B上的动点,P为x轴上的动点,则PM+PN的最小值为( )
A. 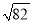 -4 B.
-4 B. 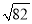 -1 C. 6-2
-1 C. 6-2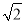 D.
D. 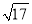 -3
-3
查看答案和解析>>
科目:初中数学 来源:北师大版七年级下册数学 第五章 生活中的轴对称 单元检测卷 题型:单选题
作已知点关于某直线的对称点的第一步是( )
A. 过已知点作一条直线与已知直线相交 B. 过已知点作一条直线与已知直线垂直
C. 过已知点作一条直线与已知直线平行 D. 不确定
B 【解析】作已知点关于某直线的对称点的第一步是过已知点作一条直线与已知直线垂直, 故选:B.查看答案和解析>>
科目:初中数学 来源:北师大版数学七年级下册 同步测试 1.2 幂的乘法与积的乘方 题型:填空题
计算:82014×(﹣0.125)2015=___________.
-0.125 【解析】试题分析:根据同底数幂的乘法,可化成指数相同的幂的乘法,根据积的乘方,可得答案.原式=82014×(﹣0.125)2014×(﹣0.125)=(﹣8×0.125)2014×(﹣0.125)=﹣0.125,查看答案和解析>>
科目:初中数学 来源:北师大版九年级上册数学全册综合测试卷二 题型:填空题
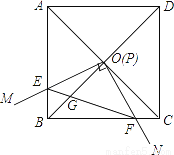
如图,边长为1的正方形ABCD的对角线AC、BD相交于点O,有直角∠MPN,使直角顶点P与点O重合,直角边PM、PN分别与OA、OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM、PN分别交AB、BC于E、F两点,连接EF交OB于点G,则下列结论中正确的是________.
(1)EF=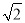 OE;(2)S四边形OEBF:S正方形ABCD=1:4;(3)BE+BF=
OE;(2)S四边形OEBF:S正方形ABCD=1:4;(3)BE+BF= 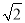 OA;(4)在旋转过程中,当△BEF与△COF的面积之和最大时,AE=
OA;(4)在旋转过程中,当△BEF与△COF的面积之和最大时,AE=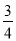 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com