
在一节数学课上,老师出示了这样一个问题让学生探究:
已知:如图,在△ABC中,点D是BA边延长线上一动点,点F在BC上,且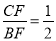 ,连接DF交AC于点E.
,连接DF交AC于点E.
(1)如图1,当点E恰为DF的中点时,请求出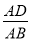 的值;
的值;
(2)如图2,当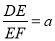 (a>0)时,请求出
(a>0)时,请求出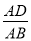 的值(用含a的代数式表示)
的值(用含a的代数式表示)
思考片刻后,同学们纷纷表达了自己的想法:
甲:过点F作FG∥AB交AC于点G,构造相似三角形解决问题;
乙:过点F作FG∥AC交AB于点G,构造相似三角形解决问题;
丙:过点D作DG∥BC交CA延长线于点G,构造相似三角形解决问题;
老师说:“这三位同学的想法都可以”.
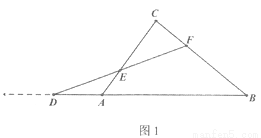
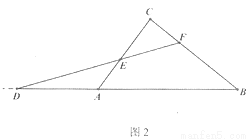
(3)请参考上面某一种想法,完成第(1)问的求解过程,并直接写出第(2)问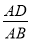 的值.
的值.
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源:重庆市江津区2017-2018学年八年级上学期第二次六校联考数学试卷 题型:解答题
先化简: 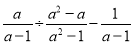 ,然后在-1、0、1、2、3中选一个
,然后在-1、0、1、2、3中选一个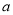 的值代入求值.
的值代入求值.
查看答案和解析>>
科目:初中数学 来源:2017年广东省河源市中考数学一诊试卷 题型:单选题
如图所示,a与b的大小关系是( )

A. a<b B. a>b C. a=b D. b=2a
A 【解析】根据数轴得到a<0,b>0, ∴b>a, 故选A查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题九年级北师大版数学试卷(C卷) 题型:单选题
如图,正方形OABC,ADEF的顶点A,D,C在坐标轴上,点F在AB上,点B,E在函数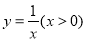 的图象上,则点E的横坐标是( )
的图象上,则点E的横坐标是( )

A. 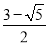 B.
B. 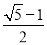 C.
C. 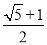 D.
D. 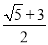
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题九年级北师大版数学试卷(C卷) 题型:单选题
关于x的一元二次方程(a-1)x2+x+a2+3a-4=0有一个实数根是x=0.则a的值为( ).
A. 1或-4 B. 1 C. -4 D. -1或4
C 【解析】本题根据一元二次方程的根的定义、一元二次方程的定义可得:查看答案和解析>>
科目:初中数学 来源:北京四中2018届上学期初中九年级期中考试数学试卷 题型:解答题
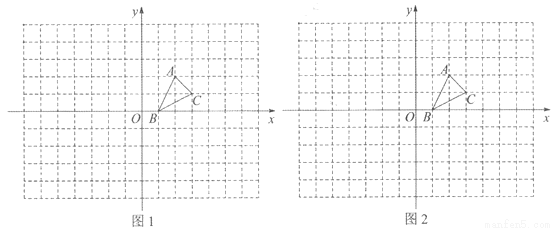
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(1,0)
(1)在图l中画出△ABC关于x轴对称的△A1B1C1;
(2)在图2中,以点O为位似中心,将△ABC放大,使放大后的△A2B2C2与△ABC的对应边的比为2:1(画出一种即可). 直接写出点A的对应点A2的坐标.
查看答案和解析>>
科目:初中数学 来源:北京四中2018届上学期初中九年级期中考试数学试卷 题型:填空题
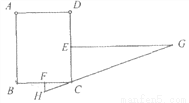
“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》,意思是说:如图,矩形城池ABCD,城墙CD长9里,城墙BC长7里,东门所在的点E,南门所在的点F分别是CD,BC的中点,EG⊥CD,EG=15里,FH⊥BC,点C在HG上,问FH等于多少里?答案是FH=________里.
查看答案和解析>>
科目:初中数学 来源:2017年甘肃省张掖市中考数学三模试卷 题型:解答题
有三张卡片(形状、大小、颜色、质地都相等),正面分别写上整式x2+1,﹣x2﹣2,3.将这三张卡片背面向上洗匀,从中任意抽取一张卡片,记卡片上的整式为A,再从剩下的卡片中任意抽取一张,记卡片上的整式为B,于是得到代数式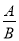 .
.
(1)请用画树状图或列表的方法,写出代数式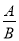 所有可能的结果;
所有可能的结果;
(2)求代数式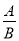 恰好是分式的概率.
恰好是分式的概率.
查看答案和解析>>
科目:初中数学 来源:2017年福建省分校九年级数学综合试卷(二) 题型:单选题
将一张正方形纸片按图A到B对折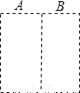 ,从C到D方向
,从C到D方向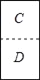 依次对折后,再沿
依次对折后,再沿 中的虚线裁剪,最后将
中的虚线裁剪,最后将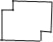 中的纸片展开铺平所得的图案应该是下图中的( )
中的纸片展开铺平所得的图案应该是下图中的( )
A. 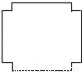 B.
B.  C.
C. 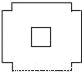 D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com