
将一张正方形纸片按图A到B对折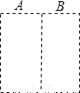 ,从C到D方向
,从C到D方向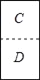 依次对折后,再沿
依次对折后,再沿 中的虚线裁剪,最后将
中的虚线裁剪,最后将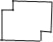 中的纸片展开铺平所得的图案应该是下图中的( )
中的纸片展开铺平所得的图案应该是下图中的( )
A. 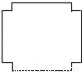 B.
B.  C.
C. 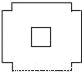 D.
D. 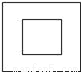
科目:初中数学 来源:北京四中2018届上学期初中九年级期中考试数学试卷 题型:解答题
在一节数学课上,老师出示了这样一个问题让学生探究:
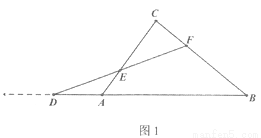
已知:如图,在△ABC中,点D是BA边延长线上一动点,点F在BC上,且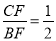 ,连接DF交AC于点E.
,连接DF交AC于点E.
(1)如图1,当点E恰为DF的中点时,请求出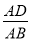 的值;
的值;
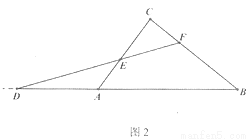
(2)如图2,当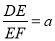 (a>0)时,请求出
(a>0)时,请求出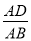 的值(用含a的代数式表示)
的值(用含a的代数式表示)
思考片刻后,同学们纷纷表达了自己的想法:
甲:过点F作FG∥AB交AC于点G,构造相似三角形解决问题;
乙:过点F作FG∥AC交AB于点G,构造相似三角形解决问题;
丙:过点D作DG∥BC交CA延长线于点G,构造相似三角形解决问题;
老师说:“这三位同学的想法都可以”.
(3)请参考上面某一种想法,完成第(1)问的求解过程,并直接写出第(2)问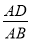 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:2017年甘肃省张掖市中考数学三模试卷 题型:单选题
如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )
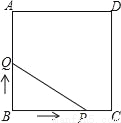
A. 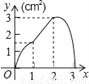 B.
B. 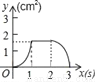 C.
C. 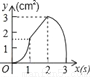 D.
D. 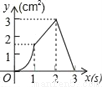
查看答案和解析>>
科目:初中数学 来源:2017年福建省分校九年级数学综合试卷(二) 题型:填空题
“圆材埋壁”是我国古代著名数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何”此问题的实质就是解决下面的问题:“如图,CD为⊙O的直径,弦AB⊥CD于点E,CE=1,AB=10,求CD的长”.根据题意可得CD的长为 .
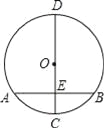
查看答案和解析>>
科目:初中数学 来源:2017年福建省分校九年级数学综合试卷(二) 题型:单选题
如图,矩形ABCD,R是CD的中点,点M在BC边上运动,E、F分别是AM、MR的中点,则EF的长随着M点的运动

A.变短 B.变长 C.不变 D.无法确定
C 【解析】 试题分析:∵E,F分别是AM,MR的中点, ∴EF=AR, ∴无论M运动到哪个位置EF的长不变,故选C.查看答案和解析>>
科目:初中数学 来源:2017年福建省分校九年级数学综合试卷(二) 题型:单选题
香港于1997年7月1日成为中华人民共和国的一个特别行政区,它的区徽图案(紫荆花)如图,这个图形( )

A. 是轴对称图形
B. 是中心对称图形
C. 既是轴对称图形,也是中心对称图形
D. 既不是轴对称图形,也不是中心对称图形
D 【解析】区徽图案(紫荆花)是通过基本图案依次旋转72°得到的,所以既不是轴对称图形,也不是中心对称图形.故选D.查看答案和解析>>
科目:初中数学 来源:2017年湖北省随州市中考数学模拟试卷 题型:解答题
计算: 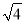 ﹣(π﹣2016)0+|
﹣(π﹣2016)0+|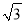 ﹣2|+2sin60°.
﹣2|+2sin60°.
查看答案和解析>>
科目:初中数学 来源:2017年黑龙江省大庆市中考数学三模试卷 题型:解答题
在2014年“元旦”前夕,某商场试销一种成本为30元的文化衫,经试销发现,若每件按34元的价格销售,每天能卖出36件;若每件按39元的价格销售,每天能卖出21件.假定每天销售件数y(件)是销售价格x(元)的一次函数.
(1)直接写出y与x之间的函数关系式y= .
(2)在不积压且不考虑其他因素的情况下,每件的销售价格定为多少元时,才能使每天获得的利润P最大?
(1);(2)38. 【解析】 试题分析:(1)设y与x满足的函数关系式为y=kx+b,由题意可列出k和b的二元一次方程组,解出k和b的值即可; (2)根据题意:每天获得的利润为:,转换为,于是求出每天获得的利润P最大时的销售价格. 试题解析:(1); (2)每天获得的利润 答:每件的销售价格定为38元时,每天获得的利润最大. 考点:.1.二次函数的应用;...查看答案和解析>>
科目:初中数学 来源:2017年湖北省黄冈市中考数学二模试卷 题型:单选题
已知mn≠1,且5m2+2010m+9=0,9n2+2010n+5=0,则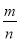 的值为( )
的值为( )
A. ﹣402 B. 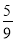 C.
C. 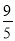 D.
D. 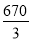
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com