
先化简: 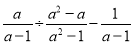 ,然后在-1、0、1、2、3中选一个
,然后在-1、0、1、2、3中选一个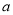 的值代入求值.
的值代入求值.
科目:初中数学 来源:2016-2017学年陕西师大附中七年级(下)第一次月考数学试卷 题型:填空题
如图,为了使一扇旧木门不变形,木工师傅在木门的背后加钉了一根木条,这样做的道理是_____.
查看答案和解析>>
科目:初中数学 来源:四川省遂宁市黄泥学校2016-2017学年上期八年级期中测评数学试卷 题型:单选题
4的平方根是( )
A. 2 B. -2 C. 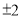 D.
D. 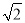
查看答案和解析>>
科目:初中数学 来源:重庆市江津区2016-2017学年八年级下学期期末考试数学试卷 题型:单选题
如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1,P2,P3,P4四个点中找出符合条件的点P,则点P有( )
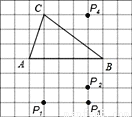
A. 1个 B. 2个 C. 3个 D. 4个
C 【解析】要使△ABP与△ABC全等,必须使点P到AB的距离等于点C到AB的距离,即3个单位长度,所以点P的位置可以是P1,P3,P4三个,故选C.查看答案和解析>>
科目:初中数学 来源:重庆市江津区2016-2017学年八年级下学期期末考试数学试卷 题型:单选题
以下列各组线段为边,能组成三角形的是( )
A. 2 cm ,3 cm,5 cm B. 3 cm,3 cm,6 cm
C. 5 cm,8 cm,2 cm D. 4 cm,5 cm,6 cm
D 【解析】A选项:2+3=5,不能组成三角形; B选项:3+3=6,不能组成三角形; C选项:2+5<8,不能够组成三角形; D选项:4+5>6,能组成三角形. 故选D.查看答案和解析>>
科目:初中数学 来源:重庆市江津区2017-2018学年八年级上学期第二次六校联考数学试卷 题型:填空题
对于正数x,规定 f(x)= 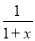 ,例如:f(4)=
,例如:f(4)= 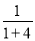 =
=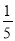 ,f(
,f(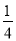 )=
)=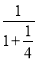 =
=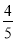 ,则f(2017)+f(2016)+…+f(2)+f(1)+f(
,则f(2017)+f(2016)+…+f(2)+f(1)+f(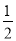 )+f(
)+f(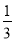 )+…+f(
)+…+f(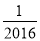 )+f(
)+f(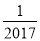 )= .
)= .
查看答案和解析>>
科目:初中数学 来源:重庆市江津区2017-2018学年八年级上学期第二次六校联考数学试卷 题型:单选题
分式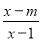 中,当
中,当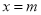 时,下列说法正确的是( )
时,下列说法正确的是( )
A. 分式的值为零 B. 分式无意义
C. 若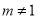 时,分式的值为零 D. 若
时,分式的值为零 D. 若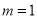 时,分式的值为零
时,分式的值为零
查看答案和解析>>
科目:初中数学 来源:2017年广东省河源市中考数学一诊试卷 题型:解答题
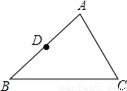
如图,已知△ABC中,D为AB的中点.
(1)请用尺规作图法作边AC的中点E,并连接DE(保留作图痕迹,不要求写作法);
(2)在(1)的条件下,若DE=4,求BC的长.
查看答案和解析>>
科目:初中数学 来源:北京四中2018届上学期初中九年级期中考试数学试卷 题型:解答题
在一节数学课上,老师出示了这样一个问题让学生探究:
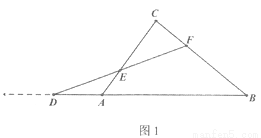
已知:如图,在△ABC中,点D是BA边延长线上一动点,点F在BC上,且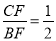 ,连接DF交AC于点E.
,连接DF交AC于点E.
(1)如图1,当点E恰为DF的中点时,请求出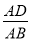 的值;
的值;
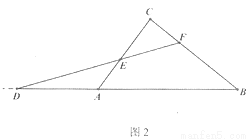
(2)如图2,当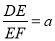 (a>0)时,请求出
(a>0)时,请求出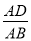 的值(用含a的代数式表示)
的值(用含a的代数式表示)
思考片刻后,同学们纷纷表达了自己的想法:
甲:过点F作FG∥AB交AC于点G,构造相似三角形解决问题;
乙:过点F作FG∥AC交AB于点G,构造相似三角形解决问题;
丙:过点D作DG∥BC交CA延长线于点G,构造相似三角形解决问题;
老师说:“这三位同学的想法都可以”.
(3)请参考上面某一种想法,完成第(1)问的求解过程,并直接写出第(2)问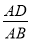 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com