
计算:20152-2×2015×2014+20142=__.
1 【解析】20152-2×2015×2014+20142=(2015-2014)2=12=1. 故答案为:1.科目:初中数学 来源:北师大版七年级数学下册4.2图形的全等练习 题型:单选题
已知:如图△ABC≌△DCB,其中点A与点D,点B与点C分别是对应顶点,如果AB=2,AC=3,CB=4,那么DC的长为( )
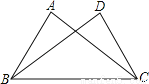
A.2 B.3 C.4 D.不确定
A 【解析】 试题分析:仔细观察图形,根据已知条件找准对应边,运用全等三角形的对应边相等即可结论. 【解析】 ∵△ABC≌△DCB,点A与点D,点B与点C分别是对应顶点, ∴CD的对应边是AB, ∴DC=AB=2. 故选A.查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下册4.1.2认识三角形 同步练习 题型:填空题
科目:初中数学 来源:北师大版七年级数学下册同步要点3.2 用关系式表示的变量间关系 题型:填空题
已知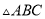 是等腰三角形,周长是
是等腰三角形,周长是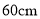 ,腰长为
,腰长为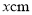 ,底为
,底为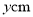 .
.
(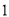 )用含
)用含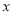 的关系式表示
的关系式表示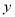 :__________.
:__________.
(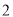 )当腰长由
)当腰长由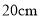 变化到
变化到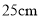 时,底边长由__________
时,底边长由__________ 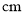 变化到__________
变化到__________ 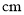 .
.
查看答案和解析>>
科目:初中数学 来源:北师大版七年级下册 第一章 整式的乘除 单元测试卷 题型:解答题
如图,要设计一幅长为3xcm、宽为2ycm的长方形图案,其中有两横两竖的彩条,横彩条的宽度为acm,竖彩条的宽度为bcm,问空白区域的面积是多少?
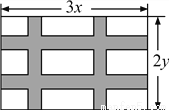
查看答案和解析>>
科目:初中数学 来源:北师大版七年级下册 第一章 整式的乘除 单元测试卷 题型:单选题
下列计算中正确的是( )
A. (-2a2b3)÷(-2ab)=a2b2
B. (-2a2b4)÷(-2ab2)=a2b2
C. 2a2bc÷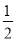 a2b=4c
a2b=4c
D. 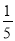 a2b3c2÷(-5abc)2=5b
a2b3c2÷(-5abc)2=5b
查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下3.2 用关系式表示的变量间关系 同步练习 题型:解答题
自行车每节链条的长度为2.5 cm,交叉重叠部分的圆的直径为0.8 cm.

(1)观察图形,填写下表:
链条的节数/节 | 2 | 3 | 4 | … |
链条的长度/cm | … |
(2)如果x节链条的长度为y(cm),那么y与x之间的关系式是什么?
(3)如果一辆某种型号自行车的链条(安装前)由60节这样的链条组成,那么这辆自行车上的链条(安装后)总长度是多少?
(1)4.2;5.9;7.6(2)即y=1.7x+0.8(3)这辆自行车上的链条(安装后)总长度为102 cm. 【解析】试题分析: (1)根据题意计算即可得到当链条节数为2、3、4时,链条的相应长度,填入表格中即可; (2)由题意可知,第1节链条长度为2.5cm,后面每增加1节链条,长度增加1.7cm,由此即可得到链条长度与链条节数之间的关系式; (3)将代入(2)中所得...查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下4.3.3 用“边角边”判定三角形全等 同步练习 题型:解答题
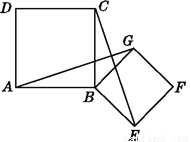
如图,四边形ABCD,四边形BEFG均为正方形,连接AG,CE.试说明:
(1)AG=CE;
(2)AG⊥CE.
查看答案和解析>>
科目:初中数学 来源:北师大版数学七年级下册第四章4.4用尺规作三角形课时练习 题型:单选题
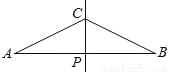
如图,直线CP是AB的中垂线且交AB于P,其中AP=2CP.甲、乙两人想在AB上取两点D、E,使得AD=DC=CE=EB,其作法如下:
甲:作∠ACP、∠BCP之角平分线,分别交AB于D、E,则D、E即为所求;
乙:作AC、BC之中垂线,分别交AB于D、E,则D、E即为所求.
对于甲、乙两人的作法,下列判断何者正确( )
A. 两人都正确 B. 两人都错误 C. 甲正确,乙错误 D. 甲错误,乙正确
D 【解析】试题解析: 甲、乙都正确, 理由是:∵CP是线段AB的垂直平分线, ∴BC=AC,∠APC=∠BPC=90°, ∵AC=2CP, ∴∠A=30°, ∴∠ACP=60°, ∵CD平分∠ACP, ∴∠ACD=∠ACP=30°, ∴∠ACD=∠A, ∴AD=DC, 同理CE=BE, 即D、E为所求; ∵D在A...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com