
在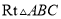 中,
中, 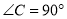 ,斜边长为
,斜边长为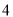 ,
, 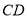 为
为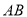 边上中线,则
边上中线,则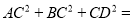 __________.
__________.
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案科目:初中数学 来源:浙江省2017学年第一学期七年级期末检测数学试卷卷 题型:单选题
如图,在数轴上,A1,P两点表示的数分别是-1,-2,作A1关于原点O对称的点得A2,作A2关于点P对称的点得A3,取线段A1A3的中点M1,作M1关于原点O对称的点得A4,作A4关于点P对称的点得A5,取线段A1A5的中点M2,……依此规律,则A8表示的数是( )

A. 4.25 B. 4.5 C. 4. 75 D. 5
B 【解析】试题解析:∵点表示-1,点表示-2, 关于点对称, ∴表示1, 同理可知: 表示-5, 表示3, 表示-7, 表示4, 表示-6, 表示4.5. 故选B.查看答案和解析>>
科目:初中数学 来源:浙江省杭州市下城区安吉路良渚实验初三上期中数学试卷 题型:解答题
(本小题满分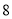 分)
分)
如图, 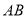 是⊙
是⊙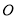 的直径,点
的直径,点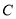 是⊙
是⊙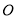 上一点,连接
上一点,连接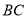 ,
, 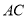 ,
, 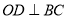 于
于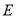 .
.
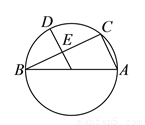
(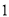 )求证:
)求证: 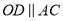 .
.
(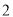 )若
)若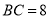 ,
, 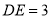 ,求⊙
,求⊙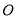 的直径.
的直径.
查看答案和解析>>
科目:初中数学 来源:浙江省杭州市下城区安吉路良渚实验初三上期中数学试卷 题型:单选题
若二次函数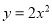 的图象经过点
的图象经过点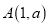 ,则
,则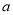 的值为( ).
的值为( ).
A. 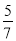 B.
B. 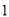 C.
C. 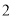 D.
D. 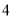
查看答案和解析>>
科目:初中数学 来源:浙江省杭州市余杭区英特外国语学校2017-2018学年八年级上学期期中数学试卷 题型:解答题
定义一种新运算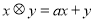 .
.
(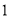 )若
)若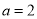 ,求
,求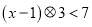 的解,并写出所有自然数解;
的解,并写出所有自然数解;
(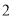 )若关于
)若关于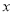 的不等式
的不等式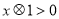 的解与(
的解与(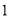 )中不等式的解相同,求
)中不等式的解相同,求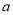 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:浙江省杭州市余杭区英特外国语学校2017-2018学年八年级上学期期中数学试卷 题型:单选题
如图, 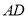 是
是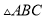 的角平分线,
的角平分线, 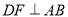 ,垂足为
,垂足为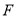 ,
, 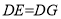 ,
, 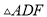 和
和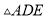 的面积分别为
的面积分别为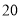 和
和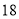 ,则
,则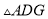 的面积为( ).
的面积为( ).
A. 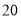 B.
B. 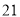 C.
C. 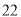 D.
D. 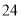
查看答案和解析>>
科目:初中数学 来源:浙江省杭州市余杭区英特外国语学校2017-2018学年八年级上学期期中数学试卷 题型:单选题
下列图形:①有两个角相等的三角形;②圆;③正方形;④直角三角形,其中一定是轴对称图形的个数是( )
A. 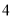 个 B.
个 B. 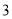 个 C.
个 C. 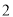 个 D.
个 D. 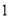 个
个
查看答案和解析>>
科目:初中数学 来源:江苏省连云港市灌南县私立新知双语学校2018届九年级(上)期中数学模拟试卷 题型:填空题
一元二次方程x(x﹣2)=x的根是_____.
x1=0,x2=3 【解析】整理方程,得x2﹣3x=0, ∴x(x﹣3)=0, 解得x1=0,x2=3.查看答案和解析>>
科目:初中数学 来源:浙江杭州下城区观成中学2018届九年级上学期期中数学试卷 题型:填空题
如图,有长为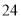 米的篱笆,一边利用墙(墙的最大可用长度为
米的篱笆,一边利用墙(墙的最大可用长度为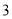 米),围成一个由两个长方形组成的花圃,当花圃的边
米),围成一个由两个长方形组成的花圃,当花圃的边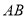 为__________米时,围成的花圃面积最大,最大面积为__________平方米.
为__________米时,围成的花圃面积最大,最大面积为__________平方米.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com