练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，在四边形ABCD中，∠DAB=∠ABC=90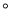,AD∥BC,AB=BC,E是AB的中点，CE⊥BD.

    (1)求证：BE=AD；

    (2)求证：AC是线段ED的垂直平分线;

    (3)△DBC是等腰三角形吗？并说明理由．

    （1）详见解析；（2）详见解析；（3）详见解析. 【解析】试题分析：（1）利用已知条件证明△BAD≌△CBE(ASA)，根据全等三角形的对应边相等即可得到结论； （2）证明AD=AE，根据线段垂直平分线的逆定理即可解答； （3）由△DAB≌△EBC，得到DB=EC，又由△AEC≌△ADC，得到EC=DC，所以DB=DC，即可解答． 试题解析：【解析】 (1)∵∠ABC＝9...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017-2018学年四川省自贡市七年级上学期期末考试数学试卷 题型：填空题

    若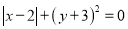，则＝________

    9 【解析】由题意，得：x-2=0， ∴x=2； y+3=0， ∴y=-3． ∴yx=（-3）2=9． 故答案是：9.

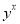    查看答案和解析>>

    科目：初中数学 来源：上海市普陀区（五四制）2017-2018学年六年级上学期期末考试数学试卷 题型：解答题

    小张计划三天看完一本240页的书，第一天看了全书的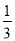，第二天看了96页，那么小张第三天应看全书的几分之几？

    小张第三天应看全书的. 【解析】试题分析：把这本书的总页数看作单位“1”，用1减去第一天看的全书的，再求出第二天看了全书的几分之几，用96÷240即可，把前两天看的分率减去，剩下的就是第三天看了全书的几分之几． 试题解析： 答：那么小张第三天应看全书的.

    查看答案和解析>>

    科目：初中数学 来源：上海市普陀区（五四制）2017-2018学年六年级上学期期末考试数学试卷 题型：填空题

    求比值：2.4∶ =_______________．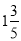

    【解析】2.4∶=2.4∶=(2.4×10)∶(1.6×10)=24:16=3:2=, 故答案为： ．

    查看答案和解析>>

    科目：初中数学 来源：上海市普陀区（五四制）2017-2018学年六年级上学期期末考试数学试卷 题型：单选题

    下列个选项中，正方形边长相同，阴影部分面积与其他三个不同的图案是（　 ）

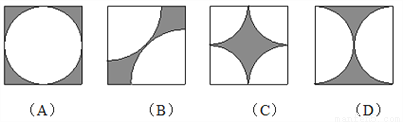
    A. （A） B. （B） C. （C） D. （D）

    B 【解析】图A阴影的面积：正方形面积?圆的面积； 图B阴影的面积：正方形的面积?对角线的一半为半圆的面积； 图C阴影的面积：正方形的面积?圆的面积； 图D阴影的面积：正方形的面积?圆的面积. 故选：B.

    查看答案和解析>>

    科目：初中数学 来源：贵州省黔南州2017-2018学年八年级上学期期末联考数学试卷 题型：解答题

    计算：

    (1) 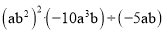(2)

    （1）；（2）. 【解析】试题分析：（1）根据单项式的乘方、乘法、除法法则计算即可； （2）先用乘法公式展开，然后去括号合并同类项即可． 试题解析：【解析】 （1）原式=； （2）原式 ．

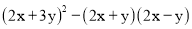
    查看答案和解析>>

    科目：初中数学 来源：贵州省黔南州2017-2018学年八年级上学期期末联考数学试卷 题型：单选题

    如图，在等边三角形ABC中，BC边上的高AD=6，E是高AD上的一个动点，F是边AB的中点，在点E运动的过程中，存在EB+EF的最小值，则这个最小值是( )

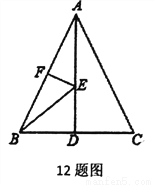
    A. 3 B. 4 C. 5 D. 6

    D 【解析】【解析】 连接CF．∵等边△ABC中，AD是BC边上的中线，∴AD是BC边上的高线，即AD垂直平分BC，∴EB=EC．当C、F、E三点共线时，EF+EC=EF+BE=CF．∵等边△ABC中，F是AB边的中点，∴AD=CF=6，∴EF+BE的最小值为6．故选D．

    查看答案和解析>>

    科目：初中数学 来源：山东省青岛市2017-2018学年上学期期末考试八年级数学试卷 题型：解答题

    如图，点C，D在线段BF上，AB∥DE，AB=DF，∠A=∠F．求证：BC=DE．

    证明见解析． 【解析】 试题分析：由可得，又，则可得，则 试题解析：在和中，

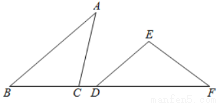
    查看答案和解析>>

    科目：初中数学 来源：河南省商丘市2017-2018学年上期七年级数学期末第一次模拟检测试卷 题型：解答题

    点O为直线AB上一点，过点O作射线OC，使∠BOC=65°，将一直角三角形的直角三角板的直角顶点放在点O处.

    （1）如图1，将三角板MON的一边ON与射线OB重合，则∠MOC=___________；

    （2）如图2，将三角板MON绕点O逆时针旋转一定角度，此时OC是∠MOB的角平分线，求旋转角∠BON和∠CON的度数；

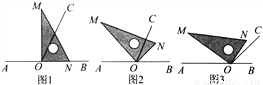
    （3）将三角板MON绕点O逆时针旋转至图3时，∠NOC=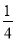∠AOM，求∠NOB的度数.

    （1）25°（2）25°（3）70° 【解析】试题分析：（1）根据∠MON和∠BOC的度数可以得到∠MON的度数； （2）根据角平分线的性质，由∠BOC=65°，可以求得∠BOM的度数，然后由∠NOM-90°，可得∠BON的度数，从而得解； （3）由∠BOC=65°，∠NOM=90°，∠NOC=∠AOM，从而可求得∠NOC的度数，然后由∠BOC=65°，从而得解. 试题解析...

    查看答案和解析>>

    同步练习册答案