
代数式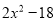 因式分解,结果正确的是( )
因式分解,结果正确的是( )
A. 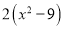 B.
B. 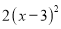 C. 2(x+3)(x-3) D. 2(x+9)(x-9)
C. 2(x+3)(x-3) D. 2(x+9)(x-9)
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2017-2018学年八年级数学下册(人教版):期中检测题 题型:单选题
如图,△ABC中,AC的垂直平分线分别交AC、AB于点D、F,BE⊥DF交DF的延长线于点E,已知∠A=30°,BC=2,AF=BF,则四边形BCDE的面积是( )
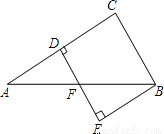
A.2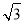 B.3
B.3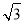 C.4 D.4
C.4 D.4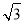
查看答案和解析>>
科目:初中数学 来源:2017-2018学年山东省济宁市嘉祥县九年级(上)月考数学试卷 题型:填空题
已知一个直角三角形的两条直角边的长恰好是方程x2﹣6x=8(x﹣6)的两个实数根,那么这个直角三角形的内切圆半径为_____.
2 【解析】x²?6x=8x-48, , (x?6)(x?8)=0, 解得x=6,x=8; 所以直角三角形的两条直角边为:6、8, 由勾股定理得:斜边长=; 所以直角三角形的内切圆半径长为 , 故答案为:2.查看答案和解析>>
科目:初中数学 来源:山东省淄博市2018届九年级上学期期中考试数学试卷 题型:解答题
解下列方程:(1)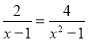
(2)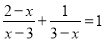
查看答案和解析>>
科目:初中数学 来源:山东省淄博市2018届九年级上学期期中考试数学试卷 题型:填空题
分解因式: 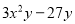 =_______________
=_______________
查看答案和解析>>
科目:初中数学 来源:山东省淄博市2018届九年级上学期期中考试数学试卷 题型:单选题
下列图案中属于旋转的是( )

A. A B. B C. C D. D
C 【解析】∵第(1)幅图案属于旋转;第(2)幅图案属于平移;第(3)幅图案属于旋转;第(4)幅图案属于旋转; ∴属于旋转的是图案是(1)、(3)、(4). 故选C.查看答案和解析>>
科目:初中数学 来源:上海市崇明区2018届九年级上学期期末调研测试数学试卷 题型:解答题
如图,CD为⊙O的直径,CD⊥AB,垂足为点F,AO⊥BC,垂足为点E,CE=2.
(1)求AB的长;
(2)求⊙O的半径.
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/13/1923086297137152/1923946164551680/STEM/edc8c851f08548f08f9e61b4dab2d43e.png]
(1)AB=4;(2)⊙O的半径是. 【解析】试题分析:(1)由, 得, ,结合可证.从而AF=CE,故可求得AB的长; (2)由垂径定理得BE=CE,故BE=AB,从而∠A=30°,在直角三角形AFO中即可求出AO的值. 试题解析:(1)∵, ∴ 在中 ∴ ∴ ∵, ∴ ∵是的直径, ∴ ∴. (2) ∵是的半径, ,...查看答案和解析>>
科目:初中数学 来源:上海市崇明区2018届九年级上学期期末调研测试数学试卷 题型:单选题
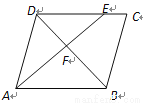
如图,在平行四边形ABCD中,点E在边DC上, 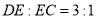 ,联结AE交BD于点F,那么
,联结AE交BD于点F,那么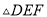 的面积与
的面积与 的面积之比为( )
的面积之比为( )
A. 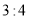 B.
B. 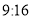 C.
C. 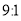 D.
D. 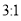
查看答案和解析>>
科目:初中数学 来源:河南省商丘市2017-2018学年上期九年级数学期末第一次模拟试卷 题型:解答题
如图,矩形EFGH内接于△ABC,且边FG落在BC上,若AD⊥BC,BC=3,AD=2,EF=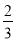 EH,求EH的长.
EH,求EH的长.
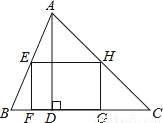
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com