
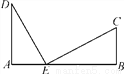
如图,铁路上A,B两点相距25 km,C,D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=15 km,CB=10 km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少千米处?
科目:初中数学 来源:2018年春人教版八年级数学下册(广西)期末测试 题型:填空题
如图,Rt△ABC中,∠ACB=90°,AC=2,BC=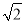 .分别以AB,AC,BC为边,向外作正方形ABDE,正方形ACFG,正方形BCMN,连接GE,DN.则图中阴影部分的总面积是____________.
.分别以AB,AC,BC为边,向外作正方形ABDE,正方形ACFG,正方形BCMN,连接GE,DN.则图中阴影部分的总面积是____________.
查看答案和解析>>
科目:初中数学 来源:江西省2017-2018学年度八年级第三次月考数学试卷 题型:单选题
如图,在四边形ABCD中,对角线AC平分∠BAD,AB>AD,下列结论中正确的是( )
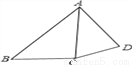
A. AB﹣AD>CB﹣CD B. AB﹣AD=CB﹣CD
C. AB﹣AD<CB﹣CD D. AB﹣AD与CB﹣CD的大小关系不确定
A 【解析】如图,在AB上截取AE=AD,连接CE. ∵AC平分∠BAD, ∴∠BAC=∠DAC, 又AC是公共边, ∴△AEC≌△ADC(SAS), ∴AE=AD,CE=CD, ∴AB-AD=AB-AE=BE,BC-CD=BC-CE, ∵在△BCE中,BE>BC-CE, ∴AB-AD>CB-CD. 故选A.查看答案和解析>>
科目:初中数学 来源:2017年广西南宁八中中考数学五模试卷 题型:单选题
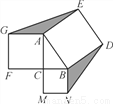
将边长为3cm的正三角形各边三等分,以这6个分点为顶点构成一个正六边形,则这个正六边形的面积为( )
A. 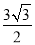 cm2 B.
cm2 B. 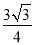 cm2 C.
cm2 C. 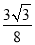 cm2 D.
cm2 D. 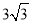 cm2
cm2
查看答案和解析>>
科目:初中数学 来源:2017年广西南宁八中中考数学五模试卷 题型:单选题
下列计算正确的是( )
A. a2•a3=a6 B. (a+b)(a﹣2b)=a2﹣2b2
C. (ab3)2=a2b6 D. 5a﹣2a=3
C 【解析】试题分析:根据同底数幂的乘法法则、多项乘以多项式的法则、积的乘方和幂的乘方法则以及代理商的运算法则逐项进行计算,即可求得答案. 试题解析:A、a2•a3=a5,故本选项错误; B、(a+b)(a-2b)=a2—ab-2b2,故本选项错误; C、(ab3)2=a2b6,本选项正确; D、5a-2a=3a,故本选项错误. 故选C.查看答案和解析>>
科目:初中数学 来源:山西省2017-2018学年八年级上期末模拟数学试卷 题型:填空题
如图,已知AB=BC,要使△ABD≌△CBD,还需添加一个条件,你添加的条件是 ________ (只需写一个,不添加辅助线)
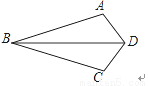
查看答案和解析>>
科目:初中数学 来源:山西省2017-2018学年八年级上期末模拟数学试卷 题型:填空题
如图所示的一块地,已知AD=4m,CD=3m,∠ADC=90°,AB=13m,BC=12m,求这块地的面积.
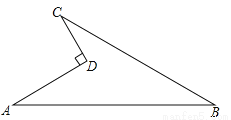
查看答案和解析>>
科目:初中数学 来源:2016-2017学年黑龙江省哈尔滨市松北区2017届九年级上学期期末数学试卷 题型:解答题
如图,是由边长为1的小正方形构成的网格,各个小正方形的顶点称之为格点,点A、C、E、F均在格点上,根据不同要求,选择格点,画出符合条件的图形:
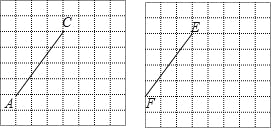
(1)在图1中,画一个以AC为一边的△ABC,使∠ABC=45°(画出一个即可);
(2)在图2中,画一个以EF为一边的△DEF,使tan∠EDF=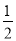 ,并直接写出线段DF的长.
,并直接写出线段DF的长.
查看答案和解析>>
科目:初中数学 来源:黑龙江省密山市2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
点M(5,y)与点N(x、-6)关于x轴对称,则x、y的值分别为( )
A. 5,-6 B. 5,6 C. -5,-6 D. -5,6
B 【解析】已知点M(5,y)与点N(x、-6)关于x轴对称,可得x=5,y=6,故选B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com