练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    在平面直角坐标系中，点（4，﹣5）关于x轴对称点的坐标为（ ）

    A. （4，5） B. （﹣4，﹣5） C. （﹣4，5） D. （5，4）

    A 【解析】平面直角坐标系中任意一点P（x，y），关于x轴的对称点的坐标是（x，-y），即关于纵轴的对称点，横坐标不变，纵坐标互为相反数，这样就可以求出对称点的坐标． 【解析】 根据关于x轴对称点的坐标特点，可得 点（4，﹣5）关于x轴对称点的坐标为（4，5）． 故选A．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北师大版九年级下册数学 第二章 二次函数 单元检测卷 题型：单选题

    抛物线y=x2+bx+c图象向右平移2个单位再向下平移3个单位，所得图象的解析式为y=x2﹣2x﹣3，则b、c的值为（   ）

    A. b=2，c=2 B. b=2，c=0 C. b=﹣2，c=﹣1 D. b=﹣3，c=2

    B 【解析】试题分析：二次函数图像的平移法则为：上加下减，左加右减． ，则反向平移后所得的解析式为： ，即b=2，c=0，故本题选B．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年九年级数学北师大版上册 第2章 一元二次方程 单元测试卷 题型：填空题

    已知关于x的一元二次方程x2﹣2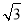x+3k=0有两个相等的实数根，则k的值是 ．

    1 【解析】 试题分析：根据方程有两个相等的实数根可得出△==0，列出关于k的方程，求出k=1．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年八年级数学北师大版上册 第1-4章综合测试卷 题型：解答题

    已知x－9的平方根是±3，x＋y的立方根是3.

    (1)求x，y的值；

    (2)x－y的平方根是多少？

    (1) y＝9；(2) x－y的平方根是±3. 【解析】试题分析：(1)根据平方根和立方根的概念列出方程，解方程求出x，y的值；根(2)据平方根的概念解答即可． 试题解析：(1)∵x－9的平方根是±3， ∴x－9＝9，解得x＝18. ∵27的立方根是3， ∴x＋y＝27， ∴y＝9； (2)由(1)得x－y＝18－9＝9，9的平方根是±3， ∴x－y...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年八年级数学北师大版上册 第1-4章综合测试卷 题型：填空题

    若关于x的函数y＝(m－1)x|m|＋9是一次函数，则m的值为________．

    －1 【解析】试题解析：根据一次函数的定义可知： 解得： 故答案为：

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年八年级数学北师大版上册 第1-4章综合测试卷 题型：单选题

    如图，Rt△ABC中，AB=9，BC=6，∠B=90°，将△ABC折叠，使A点与BC的中点D重合，折痕为MN，则线段BN的长为（　　）

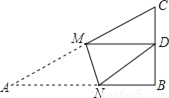
    A. B. C. 4 D. 5

    C 【解析】试题分析：设BN=x，由折叠的性质可得DN=AN=9－x， ∵D是BC的中点， ∴BD=3， 在Rt△BDN中，x2+32=（9－x）2， 解得x=4． 故线段BN的长为4． 故选C．

    查看答案和解析>>

    科目：初中数学 来源：北师大版九年级下册数学全册综合测试卷二 题型：填空题

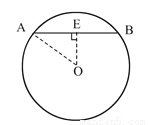
    如图，在⊙O中，弦AB的长为8cm，圆心O到AB的距离为3cm．求：⊙O的半径．

    5 cm． 【解析】连接OB，构造直角三角形BOC，根据垂径定理和弦心距得到直角三角形直角边长，利用勾股定理直接求圆的半径即可． 【解析】 连接OB，则 AC=BC=AB，∵AB=8cm，OC=3cm ∴BC=4cm 在Rt△BOC中，OB==5cm 即⊙O的半径是5cm． 故答案为5。

    查看答案和解析>>

    科目：初中数学 来源：北师大版九年级下册数学全册综合测试卷二 题型：单选题

    已知两圆相交，它们的圆心距为3，一个圆的半径是2，那么另一个圆的半径长可以是（ ）

    A. 1 B. 3 C. 5 D. 7

    B 【解析】两圆相交时，两半径之差<圆心距<两半径之和，故选B.

    查看答案和解析>>

    科目：初中数学 来源：北师大版九年级下册数学全册综合测试卷一 题型：单选题

    已知抛物线y=﹣x2+1的顶点为P，点A是第一象限内该二次函数图象上一点，过点A作x轴的平行线交二次函数图象于点B，分别过点B、A作x轴的垂线，垂足分别为C、D，连结PA、PD，PD交AB于点E，△PAD与△PEA相似吗？（　　）

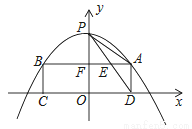
    A. 始终不相似 B. 始终相似 C. 只有AB=AD时相似 D. 无法确定

    B 【解析】试题分析：设A（x，-+1）根据题意可求出PA、PD、PE的值，从而得出PE：PA=PA：PD，又∠APE=∠DPA，因此，△PAD∽△PEA．

    查看答案和解析>>

    同步练习册答案