
在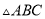 中,
中, 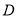 为
为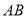 边上一点,
边上一点, 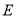 为
为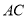 边上一点,
边上一点, 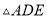 与
与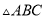 相似,己知
相似,己知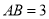 ,
, 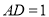 ,
, 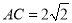 ,则
,则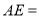 __________.
__________.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:山东省2018届九年级上学期第三次月考数学试卷 题型:解答题
不透明的袋中装有3个大小相同的小球,其中两个为白色,一个为红色,随机地从袋中摸取一个小球后放回,再随机地摸取一个小球,(用列表或树形图求下列事件的概率)
(1)两次取的小球都是红球的概率;
(2)两次取的小球是一红一白的概率.
(1);(2). 【解析】 试题分析:(1)用列表法列举出所有情况,看所求的情况与总情况的比值即可得答案, (2)由(1)的图表,可得要求的情况,与总情况作比即可得答案. 试题解析:(1)根据题意,有 两次取的小球都是红球的概率为; (2)由(1)可得,两次取的小球是一红一白的有4种;故其概率为.查看答案和解析>>
科目:初中数学 来源:湖南省衡阳市2017-2018学年八年级上期末模拟数学试卷(含答案) 题型:单选题
如图,数轴上点p表示的数可能( )
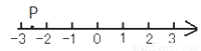
A. 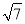 B. -
B. -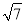 C.
C. 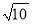 D. -
D. -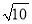
查看答案和解析>>
科目:初中数学 来源:黄金30题系列 九年级数学 大题好拿分 题型:解答题
(本题满分10分)已知关于x的方程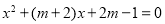 .
.
(1)求证:方程有两个不相等的实数根;
(2)是否存在实数m,使方程的两个实数根互为相反数?若存在,求出m的值;若不存在,说明理由.
(1)证明见解析;(2)m=-2 【解析】 试题分析:此题主要考查了一元二次方程根与系数的关系以及一元二次方程根的判别式,这种题型在中考中是热点问题. (1)运用一元二次方程根的判别式,当△>0,一元二次方程有两个不相等的实数根,要证明方程有两个不相等的实数根,即只要证出,△>0即可. (2)要使方程的两个实数根互为相反数,利用根与系数的关系,得出x1+x2=-=0,代入求...查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区第十三中学2017-2018学年九年级上学期期中考试数学试卷 题型:解答题
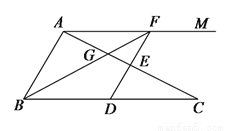
如图,已知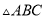 ,
, 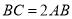 ,过点
,过点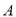 作
作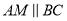 ,
, 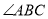 平分线分别交
平分线分别交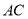 ,
, 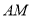 于点
于点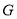 ,
, 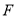 ,过点
,过点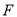 作
作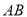 的平行线,分别交
的平行线,分别交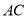 ,
, 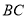 于点
于点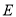 ,
, 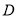 .
.
( )求证:线段
)求证:线段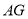 是线段
是线段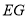 和
和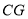 的比例中项.
的比例中项.
(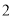 )求
)求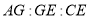 .
.
查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区第十三中学2017-2018学年九年级上学期期中考试数学试卷 题型:单选题
二次函数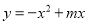 ,对称轴为直线
,对称轴为直线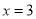 ,若关于
,若关于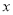 的一元二次方程
的一元二次方程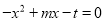 (
(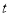 为实数)在
为实数)在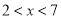 的范围内有解,则
的范围内有解,则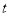 的取值范围是( ).
的取值范围是( ).
A. 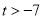 B.
B. 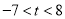 C.
C. 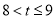 D.
D. 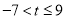
查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区第十三中学2017-2018学年九年级上学期期中考试数学试卷 题型:单选题
由5a=6b(a≠0),可得比例式( )
A、 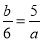 B、
B、 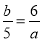 C、
C、 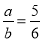 D、
D、 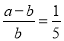
查看答案和解析>>
科目:初中数学 来源:2017年广西防城港市中考数学模拟试卷 题型:单选题
如图,在一个由4×4个小正方形组成的正方形网格中,阴影部分面积与正方形ABCD的面积比是( )
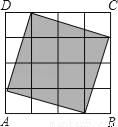
A. 5:8 B. 3:4 C. 9:16 D. 1:2
A 【解析】通过拼接,阴影部分有10个小正方形,大正方形有16个小正方形,所以面积比为10:16=5:8选A.查看答案和解析>>
科目:初中数学 来源:安徽省芜湖市教育集团2017-2018学年度上学期八年级第二次月考 题型:解答题
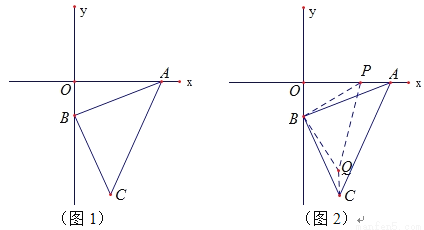
如图,已知A(3,0),B(0,-1),连接AB,过B点作AB的垂线段,使BA=BC,连接AC.
(1)如图1,求C点坐标;
(2)如图2,若P点从A点出发,沿x轴向左平移,连接BP,作等腰直角三角形△BPQ,连接CQ.求证:PA=CQ.
(3)在(2)的条件下,若C、P、Q三点共线,求此时P点坐标及∠APB的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com