
��ͼ���ھ���ABCD�У�E��AD��һ�㣬�ѡ�ABE��ֱ��BE���ۣ���A��������BC���ϵĵ�F��������ı���CDEF�;���ABCD���ƣ���ô�ı���CDEF�;���ABCD�������_________��


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ¦����¦����2017-2018ѧ�����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ���ѡ��
��֪�߶�AB= 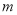 ��BC=
��BC= 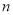 ����
����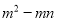 =28��
=28�� 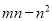 =12����
=12����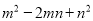 ���ڣ�������
���ڣ�������
A. 49 B. 40 C. 16 D. 9
C ����������m2-mn=28��mn-n2=12�� �ࣨm2-mn��-(mn-n2)=16�� ��=16�� ��ѡC.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�������ж�����2017--2018ѧ���һѧ����ĩ��ϰ��һ��ѧ�Ծ� ���ͣ������
�Ȼ�������ֵ����5a2+2a��1����4��3��8a+2a2��������a=��1��
��50�� �����������������ȥ���źϲ�ͬ�������ֵ������м��㼴��. ���������ԭʽ=5a2+2a��1��12+32a��8a2=��3a2+34a��13�� ��a=��1ʱ��ԭʽ=��3��34��13=��50���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�������ж�����2017--2018ѧ���һѧ����ĩ��ϰ��һ��ѧ�Ծ� ���ͣ���ѡ��
��ǽ���Ϲ̶�һ����ŵ�ľ������������Ҫ���ӵ�ö���ǣ�������
A. 1ö B. 2ö C. 3ö D. ����ö
B ���������������� ������ȷ��һ��ֱ�ߣ� ��������Ҫ2ö���ӣ� ��ѡB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���Ϻ��н�ɽ��2018����꼶��ѧ����ĩ���������ѧ�Ծ� ���ͣ������
��ͼ����֪��Rt��ABC�У���ACB=90�㣬AC > BC��CD��Rt��ABC�ĸߣ�E��AC���е㣬ED���ӳ�����CB���ӳ����ཻ�ڵ�F��
��1����֤��DF��BF��CF�ı������
��2����AB��ȡһ��G�����AE��AC=AG��AD����֤��EG��CF=ED��DF��
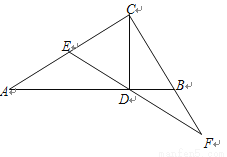
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���Ϻ��н�ɽ��2018����꼶��ѧ����ĩ���������ѧ�Ծ� ���ͣ������
������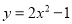 �Ķ���������_________��
�Ķ���������_________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���Ϻ��н�ɽ��2018����꼶��ѧ����ĩ���������ѧ�Ծ� ���ͣ���ѡ��
��Rt��ABC�У���ACB=90�㣬AC=12��BC=9��D��AB���е㣬G�ǡ�ABC�����ģ�����Ե�DΪԲ��DGΪ�뾶��Բ���Ե�CΪԲ�İ뾶Ϊ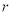 ��Բ�ཻ����ô
��Բ�ཻ����ô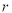 ��ȡֵ��Χ�ǣ� ��
��ȡֵ��Χ�ǣ� ��
A. 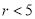 �� B.
�� B. 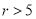 �� C.
�� C. 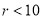 �� D.
�� D. 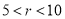 ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�人�������2017-2018ѧ�����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
����ʽ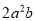 �Ĵ�����_________��
�Ĵ�����_________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������������2017-2018ѧ��ȵ�һѧ�ڰ��꼶��ĩ������ѧ�Ծ� ���ͣ������
��ͼ���ݼ����ͼ��һ���֣����С�A=30�㣬��D��б��AB���е㣬BC��DE��ֱ�ں���AC��AB=8cm��������BC��DEҪ���
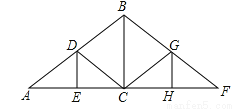
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com