
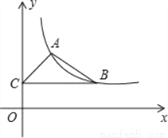
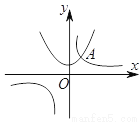
��ͼ,��ƽ��ֱ������ϵ��,����������y=kx-1��x��0����ͼ����A��1,2���͵�B��m,n����m��1��,����B��y��Ĵ��ߣ�����ΪC��
��1����÷�������������ʽ��
��2������ABC���Ϊ2ʱ,���B�����꣮
��3��PΪ�߶�AB��һ���㣨P����A��B�غϣ�,�ڣ�2���������,ֱ��y=ax��1���߶�AB���ڵ�P��ֱ��д��a��ȡֵ��Χ��

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ���㽭�����ϳ�����ʦ����������ѧ2018����꼶��ѧ�����п�����ѧ�Ծ����������� ���ͣ������
��ͼ��������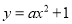 ��˫����
��˫����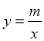 �Ľ���
�Ľ���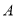 �ĺ�������
�������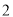 �������
�������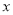 �IJ���ʽ
�IJ���ʽ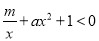 �Ľ⼯��__________��
�Ľ⼯��__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㶫ʡ��Դ�к�ƽ��2017-2018ѧ�����꼶���ϣ�������ѧ�Ծ��������棩 ���ͣ������
ij�����У�һ�����ӿ���6�ˣ����������ְڷŷ�ʽ��
��1����4�����ӣ��õ�һ�ְ��跽ʽ���������� ���ˣ��õڶ��ְ��跽ʽ���������� ���ˣ�
��2����n�����ӣ��õ�һ�ְ��跽ʽ�������� ���ˣ��õڶ��ְ��跽ʽ���������� ���ˣ��ú���n�Ĵ���ʽ��ʾ����
��3��һ�����磬����Ҫ�Ӵ�120λ�˿�ͬ�Ͳͣ���������ֻ��30�������ij��������ӿ��ã���ÿ6��ƴ��һ�Ŵ����ӣ���������Ҳ����ľ����������ѡ�����ַ�ʽ���ڷŲ�����Ϊʲô��
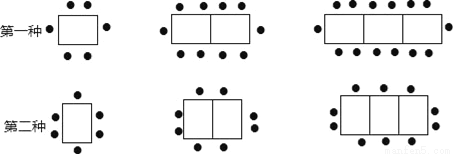
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㶫ʡ��Դ�к�ƽ��2017-2018ѧ�����꼶���ϣ�������ѧ�Ծ��������棩 ���ͣ���ѡ��
����˵���У���ȷ���ǣ��� ����
A. 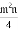 ������ʽ B. ��
������ʽ B. ��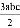 ��ϵ���ǩ�3��������3
��ϵ���ǩ�3��������3
C. 3�ǵ���ʽ D. ����ʽ2x2y��xy����ζ���ʽ
C �������������������������ĸ�Ļ���ɵĴ���ʽ��������ʽ��������һ������һ����ĸҲ��������ʽ��ϵ������һ������ʽ�еij����������ָ������ĸ��ָ��֮�ͣ�����ʽ��������ָ�������ʽ�е���ʽ�ĸ���������ʽ�и�����ʽ����ߴ�����Ϊ�������ʽ�Ĵ��������ݶ����֪������ʽ������ϵ���ǩ���������3������ʽ2x2y��xy�����ζ���ʽ����ѡ��C���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㶫ʡ��Դ�к�ƽ��2017-2018ѧ�����꼶���ϣ�������ѧ�Ծ��������棩 ���ͣ���ѡ��
��2�ľ���ֵ�ǣ�������
A. ��2 B. 2 C. ��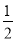 D.
D. 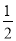
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017���������п���ѧģ���Ծ� ���ͣ������
a��b��c��ʵ������A(a��1��b)��B(a��2��c)�ڶ��κ���y��x2��2ax��3��ͼ���ϣ���b��c�Ĵ�С��ϵ��b_____c.(�á������������)
�� ����������������������κ���y��x2��2ax��3ת����y��(x-a)2-a2��3,�����ĶԳ�����x=a,�����߿������ϣ������ڶԳ����ұ�y����x�����������A��B���ڶԳ����ұ���a+1�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017���������п���ѧģ���Ծ� ���ͣ���ѡ��
��ͼ��������ֽƬABCD�ı߳�Ϊ3����E��F�ֱ��ڱ�BC��CD�ϣ���AB��AD�ֱ���AE��AF�۵�����B��Dǡ�ö����ڵ�G������֪BE=1����EF�ij�Ϊ��������
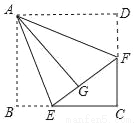
A. 1.5 B. 2.5 C. 2.25 D. 3
B �������������������DF=x����GF=DF=x��FC=3-x������BE=1�ɵã�EG=1��EC=2�������Rt��EFC�Ĺ��ɶ����ɵã�����ã�x=����EF=1+x=1+=�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�人��2017-2018ѧ�����꼶12���¿���ѧ�Ծ� ���ͣ������
��ͼ���������߶�AB=2��CD=4����A�������ϱ�ʾ������-10����C�������ϱ�ʾ������16�����߶�AB��6����λ����/����ٶ����������˶���ͬʱ�߶�CD��2����λ����/����ٶ����������˶�����B���˶����߶�CD��ʱ��P���߶�AB��һ�㣬���й�ϵʽ =3���������߶�PD�ij�Ϊ______________��
=3���������߶�PD�ij�Ϊ______________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������2017-2018ѧ�����꼶��ѧ�ڵ������¿���ѧ�Ծ����𰸲�ȫ�� ���ͣ������
�з��̽�Ӧ���⣺�ɼص��ҵ�ǰ����֮����·�Ǹ��ٹ�·��������֮һ��·����ͨ��·�����ٹ�·����ͨ��·���紦�DZ��أ�A���ڸ��ٹ�·����ͨ��·����ʻ�ٶȶ���80ǧ��/ʱ��B���ڸ��ٹ�·�ϵ���ʻ�ٶ���100ǧ��/ʱ������ͨ��·�ϵ���ʻ�ٶ���70ǧ��/ʱ��A��B�����ֱ�Ӽס�������ͬʱ����������ʻ���ڸ��ٹ�·�Ͼ������40ǧ�״���������ס�������֮��ľ����Ƕ��٣�
252 ���������������� ��ס�������֮��ľ�����xǧ�ף� ��������ã�=+�� ���x=252�� �𣺼ס�������֮��ľ�����252ǧ�ף��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com