
如图,在△ABC中,∠ABC和∠ACB的平分线相交于点F,过F作DE∥BC,交AB于点D,交AC于点E.若BD=3, DE=5,则线段EC的长是( )
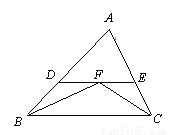
A. 3 B. 4 C. 2.5 D. 2
D 【解析】试题解析:∵∠ABC和∠ACB的平分线相交于点F, ∴∠DBF=∠FBC,∠ECF=∠BCF, 交AB于点D,交AC于点E. ∴∠DFB=∠DBF,∠CFE=∠BCF, ∴BD=DF=3,FE=CE, ∴CE=DE?DF=5?3=2. 故选D.科目:初中数学 来源:安徽省霍邱县2017-2018学年度第一学期期中考试八年级数学试卷(答案版) 题型:单选题
如图,某工厂有甲、乙两个大小相同的蓄水池,且中间有管道连通,现要向甲池中注水,若单位时间内的注水量不变,那么从注水开始,乙水池水面上升的高度h与注水时间t之间的函数关系图象可能是( )
A. 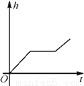 B.
B. 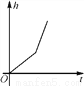 C.
C. 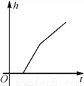 D.
D. 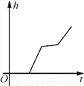
查看答案和解析>>
科目:初中数学 来源:黄金30题系列七年级数学 大题易丢分 题型:解答题
阅读解题过程,回答问题.
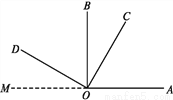
如图,OC在∠AOB内,∠AOB和∠COD都是直角,且∠BOC=30°,求∠AOD的度数.
解:过O点作射线OM,使点M,O,A在同一直线上.
因为∠MOD+∠BOD=90°,∠BOC+∠BOD=90°,所以∠BOC=∠MOD,
所以∠AOD=180°-∠BOC=180°-30°=150°.
(1)如果∠BOC=60°,那么∠AOD等于多少度?如果∠BOC=n°,那么∠AOD等于多少度?
(2)如果∠AOB=∠DOC=x°,∠AOD=y°,求∠BOC的度数.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级人教版数学试卷(B卷) 题型:解答题
先化简,再求值: 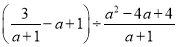 ,其中
,其中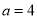 .
.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级人教版数学试卷(B卷) 题型:填空题
计算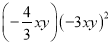 的结果为__________.
的结果为__________.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级人教版数学试卷(B卷) 题型:单选题
在△ABC与△A′B′C′中,已知∠A=∠A′,AC=A′C′,下列说法错误的是( )
A. 若添加条件AB=A′B′,则△ABC与△A′B′C′全等
B. 若添加条件∠C=∠C′,则△ABC与△A′B′C′全等
C. 若添加条件∠B=∠B′,则△ABC与△A′B′C′全等
D. 若添加条件BC=B′C′,则△ABC与△A′B′C′全等
D 【解析】试题解析:A、若添加条件AB=A′B′,可利用SAS判定△ABC≌△A′B′C′,故此选项不合题意; B、若添加条件∠C=∠C′,可利用ASA判定△ABC≌△A′B′C′,故此选项不合题意; C、若添加条件∠B=∠B′,可利用AAS判定△ABC≌△A′B′C′,故此选项不合题意; D、若添加条件BC=B′C′,不能判定△△ABC≌△A′B′C′,故此选项合题意;...查看答案和解析>>
科目:初中数学 来源:四川省广元市苍溪县东溪片区2018届九年级(上)期中数学试卷 题型:解答题
已知关于x的方程k2x2﹣2(k+1)x+1=0有两个实数根.
(1)求k的取值范围;
(2)当k=1时,设所给方程的两个根分别为x1和x2,求(x1﹣2)(x2﹣2)的值.
(1)k≥﹣且k≠0;(2)﹣3. 【解析】试题分析:(1)根据根的判别式得出k的取值范围即可; (2)把k=1代入即可得出方程,根据根与系数的关系得出x1+x2,x1x2,再代入计算即可. 试题解析: (1)根据题意得k2≠0且△=4(k+1)2﹣4k2≥0, 解得k≥﹣且k≠0; (2)k=1时方程化为x2﹣4x+1=0,则x1+x2=4,x1•x2=1, ...查看答案和解析>>
科目:初中数学 来源:四川省广元市苍溪县东溪片区2018届九年级(上)期中数学试卷 题型:单选题
解方程(x+1)2=3(1+x)的最佳方法是( )
A. 直接开平方法 B. 配方法 C. 公式法 D. 因式分解法
D 【解析】(x+1)2=3(1+x), (x+1)2﹣3(1+x)=0, (x+1)(x+1﹣3)=0, 即最好的方法是因式分解法, 故选D.查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2018届九年级12月月考数学试卷 题型:填空题
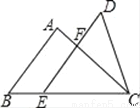
如图,已知△ABC和△DEC的面积相等,点E在BC边上,DE∥AB交AC于点F,AB=4,EF=3,则DF的长是_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com