
已知二次函数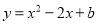 ,过点
,过点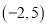 ,则
,则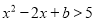 的解为__________.
的解为__________.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:山东省2018届九年级上学期第三次月考数学试卷 题型:解答题
解下列方程:
(1)2x2-4x-1=0(配方法);
(2)(x+1)2=6x+6.
(1)x1=1+,x2=1- (2) x1=-1,x2=5. 【解析】试题分析:(1)根据配方法解一元二次方程的方法,先移项,再加减一次项系数一半的平方,完成配方,再根据直接开平方法解方程即可; (2)根据因式分解法,先移项,再提公因式即可把方程化为ab=0的形式,然后求解即可. 试题解析:(1)由题可得,x2-2x=,∴x2-2x+1=. ∴(x-1)2=. ∴x-...查看答案和解析>>
科目:初中数学 来源:黄金30题系列 九年级数学 大题好拿分 题型:解答题
已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.
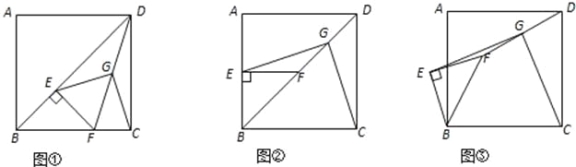
(1)求证:EG=CG;
(2)将图①中△BEF绕B点逆时针旋转45°,如图②所示,取DF中点G,连接EG,CG.
问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
(3)将图①中△BEF绕B点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?通过观察你还能得出什么结论(均不要求证明).
详见解析. 【解析】试题分析:(1)利用直角三角形斜边上的中线等于斜边的一半,可证出CG=EG. (2)结论仍然成立,连接AG,过G点作MN⊥AD于M,与EF的延长线交于N点;再证明△DAG≌△DCG,得出AG=CG;再证出△DMG≌△FNG,得到MG=NG;再证明△AMG≌△ENG,得出AG=EG;最后证出CG=EG. (3)结论依然成立.还知道EG⊥CG. (1)证明:...查看答案和解析>>
科目:初中数学 来源:黄金30题系列 九年级数学 大题好拿分 题型:解答题
如图,是由边长为1的小正方形构成的网格,各个小正方形的顶点称之为格点,点A、C、E、F均在格点上,根据不同要求,选择格点,画出符合条件的图形:
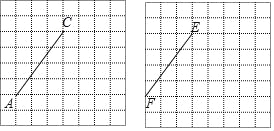
(1)在图1中,画一个以AC为一边的△ABC,使∠ABC=45°(画出一个即可);
(2)在图2中,画一个以EF为一边的△DEF,使tan∠EDF=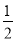 ,并直接写出线段DF的长.
,并直接写出线段DF的长.
查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区第十三中学2017-2018学年九年级上学期期中考试数学试卷 题型:解答题
如图,已知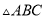 .
.
(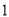 )用直尺和圆规作出⊙
)用直尺和圆规作出⊙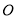 ,使⊙
,使⊙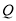 经过
经过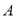 ,
, 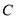 两点,且圆心
两点,且圆心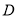 在
在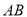 边上.(不写作法,保留作图痕迹)
边上.(不写作法,保留作图痕迹)
(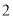 )若
)若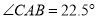 ,
, 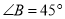 ,⊙
,⊙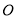 的半径为
的半径为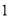 .求
.求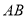 的长.
的长.

查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区第十三中学2017-2018学年九年级上学期期中考试数学试卷 题型:单选题
如图,四边形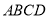 为⊙
为⊙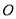 的内接四边形,弦
的内接四边形,弦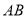 与
与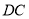 的延长线相交于点
的延长线相交于点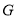 ,
, 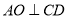 ,垂足为
,垂足为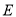 ,连接
,连接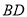 ,
, 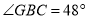 ,则
,则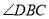 的度数为( ).
的度数为( ).

A. 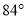 B.
B. 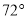 C.
C. 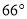 D.
D. 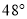
查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区第十三中学2017-2018学年九年级上学期期中考试数学试卷 题型:单选题
下列说法中,正确的是( ).
A. 买一张电影票,座位号一定是奇数
B. 投掷一枚均匀的硬币,正面一定朝上
C. 从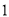 ,
, 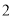 ,
, 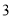 ,
, 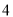 ,
, 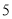 这五个数字中任意取一个数,取得奇数的可能性大
这五个数字中任意取一个数,取得奇数的可能性大
D. 三个点一定可以确定一个圆
C 【解析】A.买一张电影票,座位号不一定是奇数,故本选项错误; B.投掷一枚均匀的硬币,正面不一定朝上,故本选项错误; C.从1、2、3、4、5这五个数字中任意取一个数,取得奇数的可能性是,故本选项正确; D.三条任意长的线段不一定组成一个三角形,故本选项错误; 故选:C.查看答案和解析>>
科目:初中数学 来源:2017年广西防城港市中考数学模拟试卷 题型:单选题
不解方程,判别方程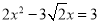 的根的情况( )
的根的情况( )
A.有两个相等的实数根
B.有两个不相等的实数根
C.有一个实数根
D.无实数根
B. 【解析】 试题分析:方程整理得,∵△=,∴方程有两个不相等的实数根.故选B.查看答案和解析>>
科目:初中数学 来源:安徽省芜湖市教育集团2017-2018学年度上学期八年级第二次月考 题型:解答题
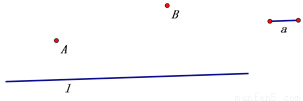
已知A、B两点在直线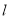 的同侧,试在
的同侧,试在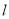 上找两点C和D(CD的长度为定值
上找两点C和D(CD的长度为定值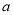 ),使得AC+CD+DB最短(保留作图痕迹,不要求写画法)。
),使得AC+CD+DB最短(保留作图痕迹,不要求写画法)。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com