练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

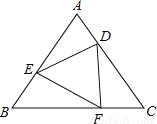
    如图，已知△ABC是正三角形，D，E，F分别是各边上的一点，且AD=BE=CF．请你说明△DEF是正三角形．

    理由见解析 【解析】【解析】 ∵△ABC为等边三角形，且AD=BE=CF， ∴AE=BF=CD， 又∵∠A=∠B=∠C=60°， ∴△ADE≌△BEF≌△CFD（SAS）， ∴DF=ED=EF， ∴△DEF是等边三角形．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017年海南省中考数学模拟试卷 题型：填空题

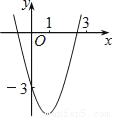
    如图，已知抛物线y=x2+bx+c经过点（0，﹣3），请你确定一个b的值，使该抛物线与x轴的一个交点在（1，0）和（3，0）之间．你确定的b的值是_____．

    1（在﹣2＜b＜2范围内的任何一个数） ． 【解析】试题分析：先把（0，-3）代入原函数y＝x 2＋bx＋c可得c=-3，所以函数变为y＝x 2＋bx-3，然后根据抛物线与x轴的一个交点在（1，0）和（3，0）之间，可知把（1，0）代入可得y=1+b-3＜0，解得b＜2；把（3，0）代入可得y=9+3b-3＞0，解得b＞-2；由此可知b的范围为：-2＜b＜2，因此只要是在这个范围的数都可以....

    查看答案和解析>>

    科目：初中数学 来源：2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷（八） 题型：单选题

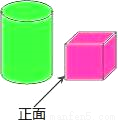
    如图，小明从正面观察一个圆柱体邮筒和一个正方体箱子，看到的是（　　）

    A. B. C. D.

    C 【解析】试题解析：从正面可看到一个长方形和正方形，故选C．

    查看答案和解析>>

    科目：初中数学 来源：2017年山东省临沂市中考数学二模试卷（一） 题型：单选题

    如图，填在各方格中的三个数之间均具有相同的规律，根据此规律，n的值是（　　）

    A. 56 B. 63 C. 70 D. 77

    C 【解析】试题解析：从方格上方的数的数1、3、5、可以推出m=7， 第一个方格中：4=1×2+2， 第二个方格中：18=3×4+6， 第三个方格中：40=5×6+10， ∴第四个方格中：n=7×8+14=70． 故选C．

    查看答案和解析>>

    科目：初中数学 来源：2017年山东省临沂市中考数学二模试卷（一） 题型：单选题

    在一次中学生田径运动会上，参加男子跳高的15名运动员的成绩如表：这些运动员跳高成绩的中位数和众数分别是（　　）

    跳高成绩（m）

    1.50

    1.55

    1.60

    1.65

    1.70

    1.75

    跳高人数

    1

    3

    2

    3

    5

    1

    A. 1.65，1.70 B. 1.70，1.65 C. 1.70，1.70 D. 3，5

    A 【解析】试题解析：跳高成绩为170的人数最多，故跳高成绩的众数为170； 共15名学生，中位数落在第8名学生处，第8名学生的跳高成绩为165，故中位数为165； 故选A.

    查看答案和解析>>

    科目：初中数学 来源：黄金30题系列 八年级数学 大题好拿分 题型：解答题

    如图，点C在线段AB上，AD∥EB，AC=BE，AD=BC，CF平分∠DCE．试探索CF与DE的位置关系，并说明理由．

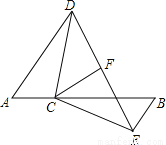
    CF⊥DE，CF平分DE（三线合一）． 【解析】试题分析：根据平行线性质得出∠A=∠B，根据SAS证△ACD≌△BEC，推出DC=CE，根据等腰三角形的三线合一定理推出即可． 【解析】 CF⊥DE，CF平分DE，理由是： ∵AD∥BE， ∴∠A=∠B， 在△ACD和△BEC中 ， ∴△ACD≌△BEC（SAS）， ∴DC=CE， ∵CF平分∠...

    查看答案和解析>>

    科目：初中数学 来源：黄金30题系列 八年级数学 大题好拿分 题型：解答题

    △ABC的三边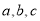满足满足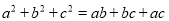，判断△ABC的形状并加以说明。

    等边三角形，理由见解析. 【解析】试题分析：将已知等式利用配方法进行变形，再利用非负数的性质求出a-b=0，b-c=0，c-a=0，即可判断出△ABC的形状． 试题解析：△ABC为等边三角形； ∵a2+b2+c2=ab+bc+ac， ∴a2+b2+c2?ab?bc?ac=0， ∴2a2+2b2+2c2?2ab?2bc?2ac=0， a2+b2?2ab+b2+c2...

    查看答案和解析>>

    科目：初中数学 来源：山东省2017-2018学年八年级上学期期中考试数学试卷 题型：单选题

    在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（　　）

    A. B. C. D.

    A 【解析】试题解析： 是轴对称图形. 故选A.

    查看答案和解析>>

    科目：初中数学 来源：湖南省衡阳市2017-2018学年八年级上期末模拟数学试卷（含答案） 题型：单选题

    下列长度的各组线段中，能够组成直角三角形的是 ( )

    A．5，6，7 　　 B．5，11，12 　　C．7，20，25 　　 D．8，15，17

    D 【解析】A、∵52+62≠72，故不能围成直角三角形，此选项错误； B、∵52+112≠122，故不能围成直角三角形，此选项错误． C、∵72+202≠52，故不能围成直角三角形，此选项错误； D、∵82+152=172，能围成直角三角形，此选项正确； 故选D．

    查看答案和解析>>

    同步练习册答案