练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    （1）计算：﹣13+20170×﹣×；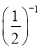

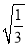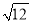    （2）解不等式组： ．

    （1）-1；（2）x＜1． 【解析】试题分析：（1）根据零指数幂、负整数指数幂的意义和二次根式的乘法法则运算； （2）分别解两个不等式得到和，然后根据同小取小确定不等式组的解集． 试题解析：（1）原式 （2） 解不等式①得： 解不等式②得： 所以不等式组的解集为：
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷（八） 题型：单选题

    已知⊙O1与⊙O2相切，若⊙O1的半径为1，两圆的圆心距为5，则⊙O2的半径为【 】

    A. 4 B. 6 C. 3或6 D. 4或6

    D 【解析】分析：由⊙O1与⊙O2相切，若⊙O1的半径为1，两圆的圆心距为5，即可分别从⊙O1与⊙O2内切或外切去分析，然后根据两圆位置关系与圆心距d，两圆半径R，r的数量关系间的联系即可求得答案． 解答：【解析】 ∵⊙O1与⊙O2相切，⊙O1的半径为1，两圆的圆心距为5， 若⊙O1与⊙O2内切，则⊙O2的半径为：5-1=4， 若⊙O1与⊙O2外切，则⊙O2的半径为：5+...

    查看答案和解析>>

    科目：初中数学 来源：黄金30题系列 八年级数学 大题好拿分 题型：解答题

    已知：a，b，c分别为△ABC的三条边的长度，请用所学知识说明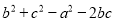： 是正数、负数或零。

    见解析 【解析】试题分析：根据三角形三边关系可知b﹣（a+c）＜0，a+b﹣c＞0，再由所给的式子进行因式分解可以整体代入判断出结果. 试题解析：根据三角形的三边关系，得b﹣（a+c）＜0，a+b﹣c＞0， ∴==（b﹣c﹣a）（b﹣c+a）＜0， 即是负数．

    查看答案和解析>>

    科目：初中数学 来源：山东省2017-2018学年八年级上学期期中考试数学试卷 题型：单选题

    如图，∠BAC=130°，若MP和QN分别垂直平分AB和AC，则∠PAQ等于( )

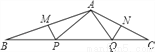
    A. 50° B. 75° C. 80° D. 105°

    C 【解析】试题分析：根据三角形内角和定理可得：∠B+∠C=180°-130°=50°，根据中垂线的性质可得：∠BAP=∠B，∠CAQ=∠C，则∠BAP+∠CAQ=∠B+∠C=50°，则∠PAQ=∠BAC-(∠BAP+∠CAQ)=130°-50°=80°，故选C．

    查看答案和解析>>

    科目：初中数学 来源：2017年海南省定安县中考数学仿真试卷（三） 题型：解答题

    如图1，二次函数y=ax2+bx+c的图象与x轴分别交于A、B两点，与y轴交于点C．若tan∠ABC=3，一元二次方程ax2+bx+c=0的两根为﹣8、2．

    （1）求二次函数的解析式；

    （2）直线l绕点A以AB为起始位置顺时针旋转到AC位置停止，l与线段BC交于点D，P是AD的中点．

    ①求点P的运动路程；

    ②如图2，过点D作DE垂直x轴于点E，作DF⊥AC所在直线于点F，连结PE、PF，在l运动过程中，∠EPF的大小是否改变？请说明理由；

    （3）在（2）的条件下，连结EF，求△PEF周长的最小值．

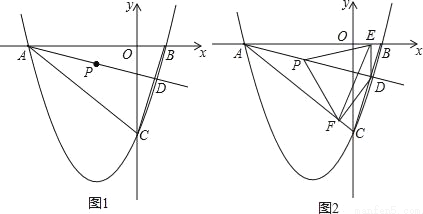
    （1）二次函数的解析式为：y=x2+x﹣6； （2）①P的运动路程为；②∠EPF的大小不会改变，理由见解析； （3）C△PEF最小值为． 【解析】试题分析：（1）由与轴分别交于A、B两点，且一元二次方程的两根为－8、2，可得点A、点B的坐标，即可得到OB的长，又由tan∠ABC=3，得到点C（0，－6），将 A、B、C的坐标代入二次函数中，即可得到二次函数解析式； （2）①...

    查看答案和解析>>

    科目：初中数学 来源：2017年海南省定安县中考数学仿真试卷（三） 题型：单选题

    甲、乙两人利用不同的交通工具，沿同一路线从A地出发前往B地，两人行驶的路程y(km)与甲出发的时间x(h)之间的函数图象如图所示．根据图象得到如下结论，其中错误的是（    ）

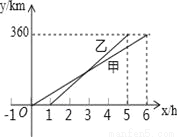
    A. 甲的速度是60km/h B. 乙比甲早1小时到达

    C. 乙出发3小时追上甲 D. 乙在AB的中点处追上甲

    D 【解析】A.根据图象得:360÷6=60km/h,故正确； B. 根据图象得，乙比甲早到1小时； C.乙的速度为：360÷4=90km/h, 设乙a小时追上甲， 90a=60（a+1） 解之得 a=2,故不正确； D. ∵90×2=180km, ∴乙在AB的中点处追上甲,故正确；

    查看答案和解析>>

    科目：初中数学 来源：2017年海南省定安县中考数学仿真试卷（三） 题型：单选题

    一个等腰三角形的两边长分别是方程x2－7x＋10＝0的两根，则该等腰三角形的周长是(　　)

    A. 12 B. 9 C. 13 D. 12或9

    A 【解析】试题分析：因式分解可得：(x－2)(x－5)=0，解得： =2， =5.当2为底，5为腰时，则三角形的周长为12；当5为底，2为腰时，则无法构成三角形.

    查看答案和解析>>

    科目：初中数学 来源：湖南省衡阳市2017-2018学年八年级上期末模拟数学试卷（含答案） 题型：填空题

    如图，在Rt△ABC中，∠C=90°，BD是三角形的角平分线，交AC于点D，AD=2.2cm，AC=3.7cm，则点D到AB边的距离是________ cm．

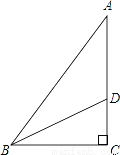
    1.5 【解析】根据角平分线的性质可得:点D到AB的距离等于点D到BC的距离,所以点D到AB边的距离等于CD=AC－AD=3.7－2.2=1.5,故答案为:1.5.

    查看答案和解析>>

    科目：初中数学 来源：2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷 题型：解答题

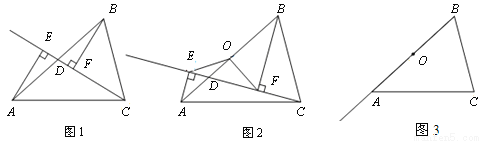
    已知点D是△ABC边AB上一动点（不与A，B重合）分别过点A，B向直线CD作垂线，垂足分别为E，F，O为边AB的中点.

    （1）如图1，当点D与点O重合时，AE与BF的位置关系是____________，OE与OF的数量关系是__________；

    （2）如图2，当点D在线段AB上不与点O重合时，试判断OE与OF的数量关系，并给予证明；

    （3）如图3，当点D在线段BA的延长线上时，此时（2）中的结论是否成立？请画出图形并写出主要证明思路．

    AE∥BF，OE=OF． OE=OF． 【解析】试题分析：（1）根据AAS推出△AEQ≌△BFQ，推出AE=BF即可； （2）延长EQ交BF于D，求出△AEQ≌△BDQ，根据全等三角形的性质得出EQ=QD，根据直角三角形斜边上中点性质得出即可； （3）延长EQ交FB于D，求出△AEQ≌△BDQ，根据全等三角形的性质得出EQ=QD，根据直角三角形斜边上中点性质得出即可． 试题...

    查看答案和解析>>

    同步练习册答案