
五边形从一顶点出发有________条对角线.
2 【解析】根据n边形从一个顶点出发可引出(n-3)条对角线可直接得到 从五边形的一个顶点可以引:5?3=2条对角线, 故答案为:2. 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:人教版九年级上册数学 22.3实际问题与二次函数(3)测试 题型:解答题
已知AB=2,C是AB上一点,四边形ACDE和四边形CBFG,都是正方形,设BC=x,
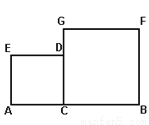
(1)AC=______;
(2)设正方形ACDE和四边形CBFG的总面积为S,用x表示S的函数解析式为S=_____.
(3)总面积S有最大值还是最小值?这个最大值或最小值是多少?
(4)总面积S取最大值或最小值时,点C在AB的什么位置?
(1)AC=2-x(0≤x≤2)(2)S=2+2(3)4(4)当x=1时,C点恰好在AB的中点上;当x=0时,C点恰好在B处;当x=2时,C点恰好在A处 【解析】试题分析:(1)、根据AB=2得出AC的长度;(2)、根据总面积等于两个正方形的面积之和得出函数解析式;(3)、根据二次函数的增减性得出面积的最大值和最小值;(4)、根据最值时x的值得出AC的长度,从而得出点C的位置. 试题解...查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 22.1.3二次函数ya(x-h)2+k的图象和性质(3)测试 题型:解答题
把二次函数y=a(x-h)2+k的图象先向左平移2个单位,再向上平移4个单位,得到二次函数y=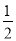 (x+1)2-1的图象.
(x+1)2-1的图象.
(1)试确定a,h,k的值;
(2)指出二次函数y=a(x-h)2+k的开口方向,对称轴和顶点坐标.
(1)a=,h=1,k=-5;(2)开口向上,对称轴为x=1,顶点坐标为(1,-5). 【解析】试题分析:(1)二次函数的平移,可以看作是将二次函数y= (x+1)2-1先向右平移2个单位,再向下平移4个单位得到二次函数y=a(x-h)2+k,然后再按二次函数图象的平移法则,确定函数解析式,即可得到结论; (2),直接根据函数解析式,结合二次函数的性质,进行回答即可. 试题分析:...查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 22.1.3二次函数ya(x-h)2+k的图象和性质(3)测试 题型:填空题
已知a≠0,
(1)抛物线y=ax2的顶点坐标为______,对称轴为______.
(2)抛物线y=ax2+c的顶点坐标为______,对称轴为______.
(3)抛物线y=a(x-m)2的顶点坐标为______,对称轴为______.
(0,0) y轴; (0,c), y轴; (m,0) 直线x=m. 【解析】【解析】 (1)抛物线y=ax2的顶点坐标为(0,0),对称轴为y轴. (2)抛物线y=ax2+c的顶点坐标为(0,c),对称轴为y轴. (3)抛物线y=a(x-m)2的顶点坐标为(m,0),对称轴为直线x=m. 故答案为:(1)(0,0) ;(2) y轴; (3) (0,c);(4).y轴; (...查看答案和解析>>
科目:初中数学 来源:人教版数学八年级上册 第11章 11.3.1 多边形同步练习(解析版) 题型:填空题
过m边形的一个顶点有7条对角线,n边形没有对角线,则m+n是________.
13 【解析】∵过m边形的一个顶点有7条对角线,n边形没有对角线, ∴m?3=7,n=3, ∴m=10,n=3, ∴m+n=10+3=13, 故答案为13.查看答案和解析>>
科目:初中数学 来源:人教版数学八年级上册 第11章 11.3.1 多边形同步练习(解析版) 题型:单选题
一个多边形的每一个内角都等于140°,那么从这个多边形的一个顶点出发的对角线的条数是( )
A. 6条 B. 7条 C. 8条 D. 9条
A 【解析】设这个多边形的边数为,则由题意可得: ,解得, ∴从此多边形的一个顶点出发可引对角线的条数为:9-3=6(条). 故选A.查看答案和解析>>
科目:初中数学 来源:人教版数学八年级上册 第11章 11.3.1 多边形同步练习(解析版) 题型:单选题
六边形共有几条对角线( )
A. 6 B. 7 C. 8 D. 9
D 【解析】根据题意得: =9, 则六边形共有9条对角线, 故选D查看答案和解析>>
科目:初中数学 来源:2017年秋四川泸县第四中学九年级第二次阶段性考试数学试卷 题型:单选题
如图2,点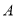 、
、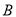 、
、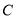 在⊙O上,
在⊙O上, 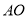 ∥
∥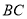 ,
, 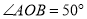 ,则
,则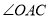 的度数是
的度数是
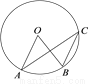
A. 25° B. 30° C. 35° D. 40°
A 【解析】∵AO ∥ BC,∴∠OAC=∠ACB, 又∠AOB与∠ACB都是弧AB所对的角, ∴∠ACB= ∠AOB=×50°=25°, ∴∠OAC的度数是25°, 故选A.查看答案和解析>>
科目:初中数学 来源:安徽省合肥市西校2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com