练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    (1)若n为正整数,且a2n=3,计算(3a3n)2÷27a4n的值;

    (2)已知(a-2)2+(b+2)2+(c-3)2=0,求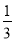a2b3c4·(3ab2c2)2÷6(a2b3c4)2的值.

    (1)1；（2）-1. 【解析】试题分析：（1）先算积的乘方，再算单项式的除法，最后把a2n=3整体代入即可；（2）先算积的乘方，再从左到右依次计算单项式的乘法和除法，然后根据偶次方的非负性求出a，b，c的值代入即可. 解:(1)原式=9a6n÷27a4n=a2n. 因为a2n=3, 所以原式=×3=1. (2)因为(a-2)2+(b+2)2+(c-3)2=0, ...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北师大版七年级数学下4.3.1 用“边边边”判定三角形全等 同步练习 题型：填空题

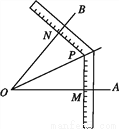
    工人师傅常用角尺平分一个任意角,做法如下:如图,已知∠AOB是任意一个角,在边OA,OB上分别截取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合,过角尺顶点P作射线OP,则OP是∠AOB的平分线,其理由是____________________.

    sss 【解析】∵OM=ON，PM=PN，OP=OP ∴△MOP≌△NOP(SSS) ∴∠MOP=∠NOP ∴OP平分∠MON (即OP是∠AOB的角平分线)

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学七年级下册第三章3.1用表格表示的变量间关系课时练习 题型：填空题

    在一个过程中，固定不变的量称为______，可以取不同的值的量称为______．

    常量 变量 【解析】根据在一个变化的过程中，数值发生变化的量称为变量；数值始终不变的量称为常量，即可得：在一个过程中，固定不变的量称为常量，可以取不同的值的量称为变量. 故答案为：常量，变量．

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学七年级下册第三章3.1用表格表示的变量间关系课时练习 题型：单选题

    如果用总长为60m的篱笆围成一个长方形场地，设长方形的面积为S（m2），周长为p（m），一边长为a（m），那么S，p，a中是变量的是（　　）

    A. S和p B. S和a C. p和a D. S，p，a

    B 【解析】∵篱笆的总长为60米， ∴周长P是定值，而面积S和一边长a是变量， 故选：B．

    查看答案和解析>>

    科目：初中数学 来源：北师大七年级下1.7 整式的除法 同步练习含答案 题型：解答题

    已知关于x的三次三项式x3+ax2-1,除以x2-x+b所得的商为x+2,余式为ax+c,求a,b,c的值.

    a=1，b=1，c=-3. 【解析】试题分析：先根据被除式=商×除式+余式，得出x3+ax2?1=(x2?x+b)(x+2)+ax+c，再运用多项式乘多项式的法则将等式右边展开，然后根据多项式相等的条件，对应项的系数相等，列方程组求解，即可得出a，b，c的值. 解:x3+ax2-1=(x2-x+b)(x+2)+(ax+c)=x3+2x2-x2-2x+bx+2b+ax+c=x3+x2+(...

    查看答案和解析>>

    科目：初中数学 来源：北师大七年级下1.7 整式的除法 同步练习含答案 题型：单选题

    下列运算正确的是(　　)

    A. (-2mn)2=-6m2n2

    B. 4x4+2x4+x4=6x4

    C. (xy)2÷(-xy)=-xy

    D. (a-b)(-a-b)=a2-b2

    C 【解析】A. ∵ (-2mn)2=4m2n2，故不正确； B. ∵4x4+2x4+x4=7x4，故不正确； C. ∵(xy)2÷(-xy)=-xy，故正确； D. ∵ (a-b)(-a-b)=b2-a2，故不正确； 故选C.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.1.2 三角形的三边关系 同步练习 题型：解答题

    把一条长为18米的细绳围成一个三角形,其中两边长分别为x米和4米.

    (1)求x的取值范围;

    (2)若围成的三角形是等腰三角形,求x的值.

    (1)5(2)x=7. 【解析】试题分析： （1）由题意可知围成的三角形的周长为18米，结合其中两边长为x米和4米，可得第三边为（18-x-4）米，再根据三角形三边间的关系列出不等式组，即可求得x的取值范围； （2）分x为底边和腰两种情况分别列出方程，可解得对应的x的值，再由三角形三边间的关系检验是否符合题意即可求得x的值. 试题解析： （1）由题意可得：18-4-x...

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.1.3 三角形的中线、角平分线 同步练习 题型：解答题

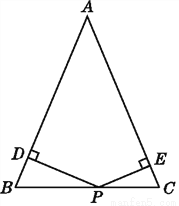
    如图,已知在△ABC中,AB=AC=4,P是BC边上任一点,PD⊥AB,PE⊥AC,D,E为垂足.若△ABC的面积为6,问:PD+PE的值能否确定?若能确定,值是多少?请说明理由.

    PD+PE的值能确定,且PD+PE=3 【解析】试题分析：可连接AP，由图得，S△ABC=S△ABP+S△ACP，代入数值，求解即可． 试题解析：【解析】 PD+PE的值能确定，且PD+PE=3．理由如下： 如图，连接AP． 由图可得S△ABC=S△ABP+S△ACP． 因为PD⊥AB，PE⊥AC，AB=AC=4，△ABC的面积为6， 所以6=×4×PD+×4...

    查看答案和解析>>

    科目：初中数学 来源：内蒙古包头市青山区2017-2018学年八年级（上）期末数学试卷 题型：填空题

    小明想知道学校旗杆有多高，他发现旗杆上的绳子垂到地面还余1m，当他把绳子下端拉开5m后，发现下端刚好接触地面，则旗杆高度为_____米．

    12 【解析】根据题意，构建数学模型为： 设绳子长AC=x，则旗杆的高为AB=x-1，而绳子拉开的距离：BC=5，根据勾股定理可得，解得x=13，所以旗杆的高度AB=12米. 故答案为：12.

    查看答案和解析>>

    同步练习册答案