
科目: 来源:安徽省2017-2018学年度九年级第三次联考数学试卷(含详细答案) 题型:填空题
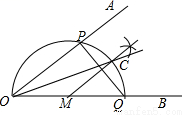
已知∠AOB,作图.
步骤1:在OB上任取一点M,以点M为圆心,MO长为半径画半圆,分别交OA、OB于点P、Q;
步骤2:过点M作PQ的垂线交弧PQ 于点C;
步骤3:画射线OC.
则下列判断:①弧CQ=弧PC;②MC∥OA;③OP=PQ;④OC平分∠AOB,
其中正确的为_______________(填序号)
查看答案和解析>>
科目: 来源:安徽省2017-2018学年度九年级第三次联考数学试卷(含详细答案) 题型:填空题
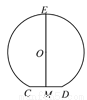
如图是一个隧道的横截面,它的形状是以点O为圆心的圆的一部分.如果M是⊙O
中弦CD的中点,EM经过圆心O交⊙O于点E,若CD=4 m,EM=6 m,则⊙O的半径为__m.
查看答案和解析>>
科目: 来源:安徽省2017-2018学年度九年级第三次联考数学试卷(含详细答案) 题型:解答题
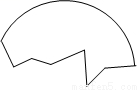
考古学家发现了一块古代圆形陶器残片如图所示,为了修复这块陶器残片,需要找出圆心.
(1)请利用尺规作图确定这块残片的圆心O;(保留作图痕迹,不写作法)
(2)写出作图的主要依据:_______________________________________________.
查看答案和解析>>
科目: 来源:安徽省2017-2018学年度九年级第三次联考数学试卷(含详细答案) 题型:解答题
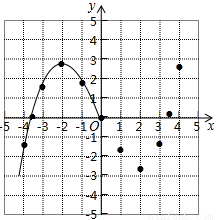
某学习小组在研究函数y=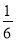 x3﹣2x的图象与性质时,已列表、描点并画出了图象的一部分.
x3﹣2x的图象与性质时,已列表、描点并画出了图象的一部分.
x | … | ﹣4 | ﹣3.5 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 3.5 | 4 | … |
y | … | ﹣ | ﹣ |
|
|
| 0 | ﹣ | ﹣ | ﹣ |
|
| … |
(1)请补全函数图象;
(2)方程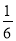 x3﹣2x=﹣2实数根的个数为 ;
x3﹣2x=﹣2实数根的个数为 ;
(3)观察图象,写出该函数的两条性质.
查看答案和解析>>
科目: 来源:安徽省2017-2018学年度九年级第三次联考数学试卷(含详细答案) 题型:解答题
党的十八大提出,倡导富强、民主、文明、和谐,倡导自由、平等、公正、法治,倡导爱国、敬业、诚信、友善,积极培育和践行社会主义核心价值观,这24个字是社会主义核心价值观的基本内容.其中:
“富强、民主、文明、和谐”是国家层面的价值目标;
“自由、平等、公正、法治”是社会层面的价值取向;
“爱国、敬业、诚信、友善”是公民个人层面的价值准则.
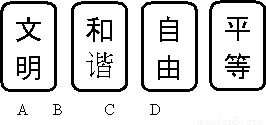
小光同学将其中的“文明”、“和谐”、“自由”、“平等”的文字分别贴在4张硬纸板上,制成如右图所示的卡片.将这4张卡片背面朝上洗匀后放在桌子上,从中随机抽取一张卡片,不放回,再随机抽取一张卡片.
(1)小光第一次抽取的卡片上的文字是国家层面价值目标的概率是 ;
(2)请你用列表法或画树状图法,帮助小光求出两次抽取卡片上的文字一次是国家层面价值目标、一次
是社会层面价值取向的概率(卡片名称可用字母表示).
查看答案和解析>>
科目: 来源:安徽省2017-2018学年度九年级第三次联考数学试卷(含详细答案) 题型:解答题
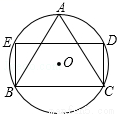
如图,等边三角形ABC内接于半径为1的⊙O,以BC为一边作⊙O的内接矩形BCDE,求矩形BCDE的面积 .
查看答案和解析>>
科目: 来源:安徽省2017-2018学年度九年级第三次联考数学试卷(含详细答案) 题型:解答题
如图,在边长为1的正方形组成的网格中建立直角坐标系,△AOB的顶点均在格点上,点O为原点,点A、B的坐标分别是A(3,2)、B(1,3).
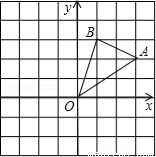
(1)将△AOB向下平移3个单位后得到△A1O1B1,则点B1的坐标为 ;
(2)将△AOB绕点O逆时针旋转90°后得到△A2OB2,请在图中作出△A2OB2,并求出这时点A2的坐标为 ;
(3)在(2)中的旋转过程中,线段OA扫过的图形的面积 .
查看答案和解析>>
科目: 来源:安徽省2017-2018学年度九年级第三次联考数学试卷(含详细答案) 题型:解答题
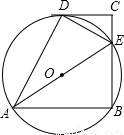
如图,在四边形ABCD中,AB∥CD,∠B=90°,AB=AD,∠BAD的平分线交BC于E,连接DE.
(1)说明点D在△ABE的外接圆上;
(2)若∠AED=∠CED,试判断直线CD与△ABE外接圆的位置关系,并说明理由.
查看答案和解析>>
科目: 来源:安徽省2017-2018学年度九年级第三次联考数学试卷(含详细答案) 题型:解答题
如图所示,在平面直角坐标系中,A、B为x轴上两点,C、D为y轴上两点,经过点A,C,B的抛物线的一部分C1与经过点A,D,B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封闭曲线称为“蛋线”.已知点C的坐标为(0, 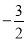 ),点M是抛物线C2:y=mx2-2mx-3m(m<0)的顶点:
),点M是抛物线C2:y=mx2-2mx-3m(m<0)的顶点:
(1)求A、B两点的坐标;
(2)求经过点A,C,B的抛物线C1的函数表达式.
(3)探究“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出点P的坐标及△PBC面积的最大值;若不存在,请说明理由.
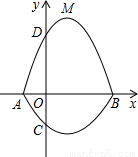
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com