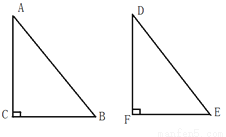
如图：在Rt△ABC和Rt△DEF中，∠C=90°，∠F=90°，BC=EF．请你添加一个条件：_____________________，使△ABC≌△DEF．

∠A=∠D(或∠B=∠E，AB=DE，AC=DF) 【解析】∵在Rt△ABC和Rt△DEF中，∠C=90°，∠F=90°，BC=EF． ∴存在下列几种添加条件的方法，使△ABC≌△DEF， ①添加∠A=∠D，结合已知可由“AAS”证得△ABC≌△DEF； ②添加∠B=∠E，结合已知可由“ASA”证得△ABC≌△DEF； ③添加AB=DE，结合已知可由“HL”证得△AB...

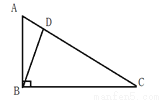
如图：在△ABC中，若∠ABC=90°，∠A=58°，又CD=CB，则∠ABD=____________．

16° 【解析】∵在△ABC中，若∠ABC=90°，∠A=58°， ∴∠C=90°-58°=32°， ∵CD=CB， ∴∠CBD=∠CDB=， ∴∠ABD=∠ABC-∠CBD=90°-74°=16°.

若一个正多边形的一个外角是60°，则这个多边形的内角和的度数是________________．

720° 【解析】∵正多边形的所有外角都是相等的， ∴当正多边形的一个外角是60°时，其余外角也都是60°， ∴该正多边形的边数为：360°60°=6， ∴这个多边形的内角和为：180°（6-2）=720°.

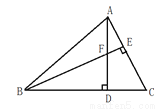
如图：在△ABC中，∠ABC=45°，AD、BE是△ABC 的高，若已知CD=5，就可得到DF=5，这样做的理论依据_________________________．

全等三角形的对应边相等 【解析】∵在△ABC中， AD、BE是△ABC 的高， ∴∠BDF=∠ADC=∠BEC=90°， ∴∠DAC+∠C=90°，∠DBF+∠C=90°， ∴∠DAC=∠DBF， ∵∠ABC=45°，∠BDF=90°， ∴∠BAD=∠ABC=45°， ∴AD=BD， ∵在△DAC和△DBF中： ， ∴△DAC≌△DBF， ...

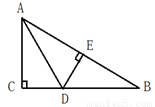
如图：△ABC中，∠C=90°，AD 平分∠BAC交CB于点D．现将直角边AC沿直线AD折叠，AC边恰好落在斜边上，且点C与斜边AB的中点E刚好重合，若CD=3，则BD=________________．

6 【解析】由折叠的性质可得，∠DEA=∠C=90°， ∴DE⊥AB， 又∵点E是AB的中点， ∴DE垂直平分AB， ∴BD=AD， ∴∠B=∠DAB， ∵AD平分∠BAC， ∴∠CAD=∠DAB=∠B， 又∵∠CAD+∠DAB+∠B=180°， ∴∠CAD=30°， ∴AD=2CD=6， ∴BD=AD=6.

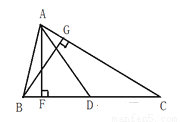
如图：△ABC的边BC的高为AF，AC边上的高为BG，中线为AD，AF=6，BC=12，BG=5．

（1）求△ABD的面积．

（2）求AC的长．

（3）△ABD和△ACD的面积有何关系．

（1）△ABD的面积=18；（2） AC=14.4；（3）S△ABD=S△ADC． 【解析】试题分析： （1）由AD是△ABC的中线可得BD=DC=BC=6，结合高AF=6可计算出△ABD的面积为18； （2）由△ABC的面积=ACBG=BCAF，及BC=12，AF=6，BG=5，可解得AC=14.4； （3）由BD=CD，△ABD中BD边上的高是AF，△ADC中DC边上的...

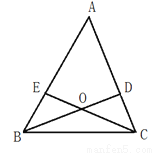
如图：在△ABC中点D、E分别在边AC、AB上，BD和CE相交于点O，有下面三个条件：①∠EBO=∠DCO，②BE=CD，③OB=OC．

（1）上述三个条件中，由哪两个条件可以判定出AB=AC．

（2）选择（1）中的一种情形，写出证明的过程．

（1）由（1）（2）或（1）（3）都可判定AB=AC；（2）证明见解析． 【解析】试题分析： （1）当①②组合时，可由“AAS”证得△EBO≌△DCO，得到OB=OC，再得∠OBC=∠OCB，再证：∠ABC=∠ACB就可得AB=AC；当①③组合时，可先由OB=OC证得∠OBC=∠OCB，再证：∠ABC=∠ACB就可得AB=AC；当②③组合时，不能证得结论； （2）在两种可选组合中...

在平面直角坐标系中有一点A，其坐标为A（3，2）回答下列问题：

（1）点A关于x轴的对称点B的坐标点为（ ）

点A关于y轴的对称点C的坐标点为（ ）

（2）若在x轴上找一点D，使DA+DC之和最短，则点D的坐标为（ ）

（3）若在x轴上找一点E，使△OAE为等腰三角形，则有____个这样的E点．

（1）B（3，-2） C（-3，2）；（2）D（0，0）；（3）有4个这样的E点． 【解析】（1）∵点A的坐标为（3，2），A与B关于轴对称、A与C关于对称， ∴点B的坐标为（3，-2），点C的坐标为（-3，2）； （2）∵点A和点B是关于轴对称的， ∴连接BC，BC与轴的交点就是所求的D点， 又∵点B和点C关于原点对称， ∴BC和轴的交点就是原点，即点D的坐标...

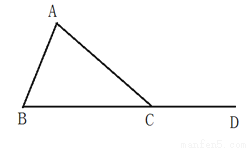
如图：∠ACD是△ABC的一个外角，CA=CB．

（1）画出∠ACD的角平分线CE．

（2）求证：CE∥AB．

（1）作图见解析；（2）证明见解析． 【解析】试题分析： （1）按要求规范的画出∠ACD的角平分线即可； （2）由CA=CB，可得∠A=∠B，由三角形外角的性质可得：∠ACD=∠A+∠B，由此可得：∠ACD=2∠A，由CE平分∠ACD可得∠ACD=2∠ACE，从而得到∠A=∠ACE，即可得AB∥CE. 试题解析： （1）画∠ACD的角平分线如下图： （2）∵CA...

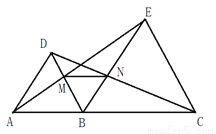
在学习了全等三角形和等边三角形的知识后，张老师出了如下一道题：如图，点B是线段AC上任意一点，分别以AB、BC为边在AC同一侧作等边△ABD和等边△BCE，连接CD、AE分别与BE和DB交于点N、M，连接MN．

(1)求证：△ABE≌△DBC．

接着张老师又让学生分小组进行探究：你还能得出什么结论？

精英小组探究的结论是：AM=DN．

奋斗小组探究的结论是：△EMB≌△CNB．

创新小组探究的结论是：MN∥AC．

（2）你认为哪一小组探究的结论是正确的？

（3）选择其中你认为正确的一种情形加以证明．

（1）证明见解析；（2）三个小组探究的结论都正确；（3）证明见解析 【解析】试题分析： （1）由△ABD和△BCE都是等边三角形可得：AB=DB，BC=BE，∠ABD=∠EBC=60°，这样可得∠ABE=∠DBC，从而可由“SAS”证得△ABE≌△DBC； （2）由△ABE≌△DBC可得∠EAB=∠CDB，而由已知条件易证∠DBN=∠ABD=60°，结合AB=DB可证△ABM≌△...