练习册

  • 练习册
  • 试题
    相关习题
     0  319313  319321  319327  319331  319337  319339  319343  319349  319351  319357  319363  319367  319369  319373  319379  319381  319387  319391  319393  319397  319399  319403  319405  319407  319408  319409  319411  319412  319413  319415  319417  319421  319423  319427  319429  319433  319439  319441  319447  319451  319453  319457  319463  319469  319471  319477  319481  319483  319489  319493  319499  319507  366461 

    科目： 来源：人教版九年级上册数学 23.2.3关于原点对称的点的坐标 测试 题型：填空题

    点A（﹣1，2）关于原点对称点B的坐标是 ．

    （1，﹣2）． 【解析】试题分析：根据关于原点对称的点的坐标特点：它们的坐标符号相反,可直接得到点A（﹣1，2）关于原点对称点B的坐标是（1，﹣2）．

    查看答案和解析>>

    科目： 来源：人教版九年级上册数学 23.2.3关于原点对称的点的坐标 测试 题型：填空题

    已知点A（﹣2m+4，3m﹣1）关于原点的对称点位于第四象限，则m的取值范围是 ．

    m＞2． 【解析】 试题分析：直接利用关于原点对称点的性质得出关于m的不等式进而求出答案． 【解析】 ∵点A（﹣2m+4，3m﹣1）关于原点的对称点位于第四象限， ∴﹣（﹣2m+4）＞0，﹣（3m﹣1）＜0， 解得：m＞2 则m的取值范围是：m＞2． 故答案为：m＞2．

    查看答案和解析>>

    科目： 来源：人教版九年级上册数学 23.2.3关于原点对称的点的坐标 测试 题型：填空题

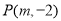    若点与点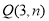关于原点对称，则= ．

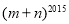    ?1 【解析】 试题分析：两点关于原点对称，则两点的横纵坐标都互为相反数，则m=－3，n=2，则=－1．

    查看答案和解析>>

    科目： 来源：人教版九年级上册数学 23.2.3关于原点对称的点的坐标 测试 题型：解答题

    如图所示的正方形网格中，△ABC的顶点均在格点上，请在所给直角坐标系中按要求画图．

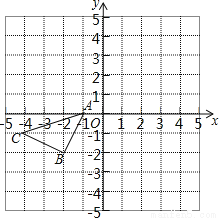
    （1）将△ABC向右平移1个单位长度，再向上平移4个单位长度，请画出平移后的△A1B1C1．

    （2）画出△ABC关于坐标原点O成中心对称的△A2B2C2．

    见解析 【解析】 试题分析：（1）直接利用平移的性质得出各点坐标，进而得出答案； （2）直接利用关于原点对称点的性质得出各点坐标，进而得出答案． 【解析】 （1）如图所示：△A1B1C1，即为所求； （2）如图所示：△A2B2C2，即为所求．

    查看答案和解析>>

    科目： 来源：数学人教版八年级上册第11章第二节与三角形有关的角第一课时同步练习 题型：单选题

    一个三角形的两个内角和小于第三个内角，这个三角形是（　　）三角形．

    A. 锐角 B. 钝角 C. 直角 D. 等腰

    B 【解析】【解析】 三角形的三角内角和等于180度，如果其中两个内角之和小于第三个内角，说明第三个内角大于90度，因此这个三角形是钝角三角形；故选B．

    查看答案和解析>>

    科目： 来源：数学人教版八年级上册第11章第二节与三角形有关的角第一课时同步练习 题型：单选题

    三角形的三个内角( )

    A、至少有两个锐角 B、至少有一个直角

    C、至多有两个钝角 D、至少有一个钝角

    A 【解析】根据三角形的内角和是180°判断即可． 【解析】 根据三角形的内角和是180°，知：三个内角可以都是60°，排除B； 三个内角可以都是锐角，排除C和D； 三角形的三个内角中至少有两个锐角，不可能有两个钝角或两个直角． 故选A． 考查了三角形的内角和定理：三角形的三个内角和是180°．

    查看答案和解析>>

    科目： 来源：数学人教版八年级上册第11章第二节与三角形有关的角第一课时同步练习 题型：单选题

    一个三角形的一个内角等于另外两个内角的和，这个三角形是（　　）

    A. 直角三角形 B. 锐角三角形 C. 钝角三角形 D. 何类三角形不能确定

    A 【解析】【解析】 三角形的一个外角等于与它不相邻的两内角之和，又一个内角也等于另外两个内角的和，由此可知这个三角形中有一个内角和它相邻的外角是相等的，且外角与它相邻的内角互补，所以有一个内角一定是90°，故这个三角形是直角三角形．故选A．

    查看答案和解析>>

    科目： 来源：数学人教版八年级上册第11章第二节与三角形有关的角第一课时同步练习 题型：单选题

    一个三角形的两个内角之和小于第三个内角，那么该三角形是（　　）

    A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 都有可能

    C 【解析】【解析】 三角形的三角内角和等于180度，如果其中两个内角之和小于第三个内角，说明第三个内角大于90度，因此这个三角形是钝角三角形；故选C．

    查看答案和解析>>

    科目： 来源：数学人教版八年级上册第11章第二节与三角形有关的角第一课时同步练习 题型：单选题

    一个三角形的三个内角的度数比是1：2：1，这个三角形是（　　）．

    A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 等腰直角三角形

    D 【解析】【解析】 最大内角=180°×=90°，另外内角=180°×=45°．故三角形为等腰直角三角形．故选D．

    查看答案和解析>>

    科目： 来源：数学人教版八年级上册第11章第二节与三角形有关的角第一课时同步练习 题型：单选题

    一个正方形和两个等边三角形的位置如图所示，若∠3=50°，则∠1＋∠2等于( )

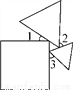
    A. 90° B. 100° C. 130° D. 180°

    B 【解析】试题分析：如图，∠1=90°-∠BAC； ∠2=120°-∠ACB； ∠3=120°-∠ABC； ∴∠1+∠2+∠3=90°-∠BAC+120°-∠ACB+120°-∠ABC=150° ∵∠3=50° ∴∠1+∠2=100° 故选B

    查看答案和解析>>

    同步练习册答案