
科目: 来源:山东省聊城市2018届九年级上学期期中考试数学试卷 题型:解答题
计算:(1)sin260°+cos260°-tan45°; (2)|-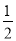 |+
|+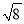 -4cos45°+2sin30°.
-4cos45°+2sin30°.
查看答案和解析>>
科目: 来源:山东省聊城市2018届九年级上学期期中考试数学试卷 题型:解答题
解方程:(1)2y2+5y=7.(公式法) (2)y2-4y+3=0(配方法)
(1)y=1或y=;(2)y=3或y=1. 【解析】试题分析:(1)整理成一般式,利用求根公式求解可得; (2)移项后,两边都加上4配成完全平方式,再开方求解可得. 【解析】 (1)原方程整理成一般式可得2y2+5y-7=0, ∵a=2,b=5,c=-7, ∴△=25-4×2×(-7)=81>0, 则y=, ∴y=1或y=; (2)∵y2-4y=-...查看答案和解析>>
科目: 来源:山东省聊城市2018届九年级上学期期中考试数学试卷 题型:解答题
如图,在边长均为l的小正方形网格纸中,△ABC的顶点,A、B、C均在格点上,O为直角坐标系的原点,点A(-1,0)在x轴上.
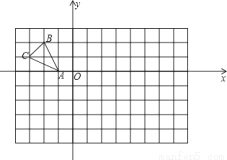
(1)以O为位似中心,将△ABC放大,使得放大后的△A1B1C1与△ABC的相似比为2:1,要求所画△A1B1C1与△ABC在原点两侧;
(2)分别写出B1、C1的坐标.
(1)画图见解析;(2)B1、C1的坐标分别为:(4,-4),(6,-2). 【解析】试题分析:(1)连接OA并延长,使OA1=2OA,同法得到其余各点,顺次连接即可; (2)根据所得图形及网格图即可得出答案. 【解析】 (1)所画图形如下所示: △A1B1C1即为所求. (2)B1、C1的坐标分别为:(4,-4),(6,-2).查看答案和解析>>
科目: 来源:山东省聊城市2018届九年级上学期期中考试数学试卷 题型:解答题
如图,在一个坡角为20°的斜坡上有一棵树,高为AB,当太阳光线与水平线成52°角时,测得该树斜坡上的树影BC的长为10m,求树高AB(精确到0.1m) (已知:sin20°≈0.342,cos20°≈0.940,tan20°≈0.364,sin52°≈0.788,cos52°≈0.616,tan52°≈1.280.供选用)
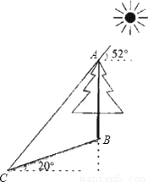
查看答案和解析>>
科目: 来源:山东省聊城市2018届九年级上学期期中考试数学试卷 题型:解答题
如图,已知AB为⊙O的直径,CD是弦,且AB⊥CD于点E.连接AC、OC、BC.
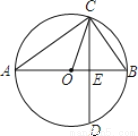
(1)求证:∠ACO=∠BCD;
(2)若BE=3,CD=8,求AB的长.
(1)证明见解析;(2)AB=. 【解析】试题分析:(1)根据圆周角定理得到∠ACB=90°,根据直角三角形的性质和等腰三角形的性质得到答案; (2)根据垂径定理得到CE的长,根据勾股定理计算即可. 【解析】 (1)∵AB为⊙O的直径, ∴∠ACB=90°, ∴∠A+∠B=90°, ∵AB⊥CD, ∴∠BCD+∠B=90°, ∴∠A=∠BCD, ...查看答案和解析>>
科目: 来源:山东省聊城市2018届九年级上学期期中考试数学试卷 题型:解答题
如图,AB是⊙O的直径,AE交⊙O于点F,且与⊙O的切线CD互相垂直,垂足为D.
(1)求证:∠EAC=∠CAB;
(2)若CD=4,AD=8,求⊙O的半径.

查看答案和解析>>
科目: 来源:山东省聊城市2018届九年级上学期期中考试数学试卷 题型:解答题
如图,小丽假期在娱乐场游玩时,想要利用所学的数学知识测量某个娱乐场地所在山坡AE的长度.她先在山脚下点E处测得山顶A的仰角是30°,然后,她沿着坡度是i=1:1(即tan∠CED=1)的斜坡步行15分钟抵达C处,此时,测得A点的俯角是15°.已知小丽的步行速度是18米/分,图中点A、B、E、D、C在同一平面内,且点D、E、B在同一水平直线上.求出娱乐场地所在山坡AE的长度.(参考数据: 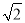 ≈1.41,结果精确到0.1米)
≈1.41,结果精确到0.1米)
查看答案和解析>>
科目: 来源:山东省聊城市2018届九年级上学期期中考试数学试卷 题型:解答题
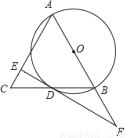
如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作EF⊥AC于点E,交AB的延长线于点F.
(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)如果AB=5,BC=6,求DE的长.
查看答案和解析>>
科目: 来源:人教版九年级上册 22.3 二次函数的应用 同步测试 题型:单选题
足球守门员大脚开出去的球的高度随时间的变化而变化,这一过程可近似地用下列哪幅图刻画( )
A. 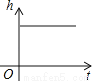 B.
B. 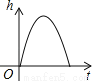 C.
C. 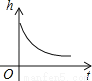 D.
D. 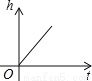
查看答案和解析>>
科目: 来源:人教版九年级上册 22.3 二次函数的应用 同步测试 题型:单选题
如图,铅球运动员掷铅球的高度y(m)与水平距离x(m)之间的函数关系式是y=﹣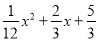 ,则该运动员此次掷铅球的成绩是( )
,则该运动员此次掷铅球的成绩是( )
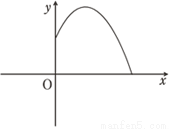
A. 6m B. 12m C. 8m D. 10m
D 【解析】试题分析:根据图示,把y=0代入y=-x2+x+可得:-x2+x+=0,解之得:x1=10,x2=-2.又x>0,解得x=10. 故选D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com