如图，△ABC中，P为AB上一点，在下列四个条件中，①∠ACP=∠B；②∠APC=∠ACB；③AC2=AP·AB；④AB·CP=AP·CB，其中能满足△APC和△ACB相似的条件是( )

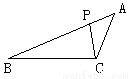
A、①②④ B、①③④    C、②③④ D、①②③

D 【解析】 试题分析：由图可得△APC和△ACB已经有一个公共角∠A，再根据相似三角形的判定方法依次分析各小题即可判断. ①∠ACP=∠B，②∠APC=∠ACB，③即，能满足； ④即，夹角应为∠B，故不能满足； 故选D.

如图，一艘潜艇在海面下500米A处测得俯角为30°的海底C处有一黑匣子发出信号，继续在同一深度直线航行4000米后，在B处测得俯角为60°的海底也有该黑匣子发出的信号，则黑匣子所在位置点C在海面下的深度为（ ）

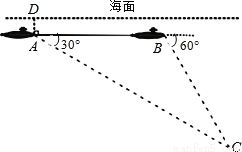
A. 2000米 B. 4000米 C. 2000米 D. （2000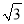+500）米

D 【解析】试题分析：由C点向AB作垂线，交AB的延长线于E点，并交海面于F点，易证∠BAC=∠BCA，所以有BA=BC．然后在直角△BCE中，利用正弦函数求出CE的长． 【解析】 由C点向AB作垂线，交AB的延长线于E点，并交海面于F点. 已知AB=4000(米),∠BAC=30°,∠EBC=60°， ∵∠BCA=∠EBC?∠BAC=30°， ∴∠BAC=∠BCA...

小明同学将一张圆桌紧靠在矩形屋子的一角，与相邻两面墙相切，她把切点记为A、B，然后，她又在桌子边缘上任取一点P（异于A、B），则∠APB的度数为（ ）

A. 45° B. 135° C. 45°或135° D. 90°或135°

C 【解析】试题分析：连接OA、OB，则∠MAO=∠MBO=90°即可求得弧AB所对的圆心角的度数，然后分P在优弧和劣弧上两种情况进行讨论，利用圆周角定理即可求解． 【解析】 连接OA、OB，则∠MAO=∠MBO=90°， 又∵∠M=90°， ∴四边形AOBM是矩形。 ∴∠AOB=90°， 当P在AB所对的优弧上时，∠P=∠AOB=45°， 则当P在劣弧...

如图，在钝角三角形ABC中，AB=6cm，AC=12cm，动点D从A点出发到B点止，动点E从C点出发到A点止．点D运动的速度为1cm/秒，点E运动的速度为2cm/秒．如果两点同时运动，那么当以点A、D、E为顶点的三角形与△ABC相似时，运动的时间是（ ）

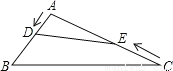
A. 4或4.8 B. 3或4.8 C. 2或4 D. 1或6

B 【解析】试题分析：根据相似三角形的性质，由题意可知有两种相似形式，△ADE∽△ABC和△ADE∽△ACB，可求运动的时间是3秒或4.8秒． 【解析】 根据题意得：设当以点A、D、E为顶点的三角形与△ABC相似时，运动的时间是x秒， ①若△ADE∽△ABC，则AD:AB=AE:AC， 即x:12?2x=x:6， 解得：x=3； ②若△ADE∽△ACB，则AD...

如图，等腰直角△ABC中，AB=AC=8，以AB为直径的半圆O交斜边BC于D，则阴影部分面积为（结果保留π）（ ）

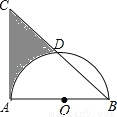
A. 16 B. 24-4π C. 32-4π D. 32-8π

B 【解析】试题分析：连接AD，因为△ABC是等腰直角三角形，故∠ABD=45°，再由AB是圆的直径得出∠ADB=90°，故△ABD也是等腰直角三角形，所以，S阴影=S△ABC-S△ABD-S弓形AD由此可得出结论． 【解析】 连接AD，OD， ∵等腰直角△ABC中， ∴∠ABD=45°. ∵AB是圆的直径， ∴∠ADB=90°， ∴△ABD也是等腰直角...

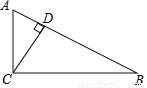
已知CD是Rt△ABC斜边上的高线，且AB=10，若BC=8，则cos∠ACD= ______ ．

【解析】试题分析：根据同角的余角相等得：∠ACD=∠B，利用同角的余弦得结论． 【解析】 ∵CD是Rt△ABC斜边上的高线， ∴CD⊥AB， ∴∠A+∠ACD=90°， ∵∠ACB=90°， ∴∠B+∠A=90°， ∴∠ACD=∠B， ∴cos∠ACD=cos∠B===， 故答案为： .

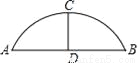
如图，某公园的一座石拱桥是圆弧形（劣弧），其跨度为24米，拱的半径为13米，则拱高CD为__米．

8 【解析】试题解析：因为跨度AB=24m，拱所在圆半径为13m， 延长CD到O，使得OC=OA，则O为圆心， 则AD=AB=12（米）， 则OA=13米， 在Rt△AOD中，DO==5， 进而得拱高CD=CO-DO=13-5=8米．

阅读下面材料：

在数学课上，老师提出如下问题：

尺规作图：作Rt△ABC，使其斜边AB=c，一条直角边BC=a．

已知线段a，c如图．

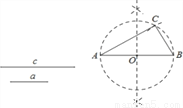
小芸的作法如下：

① 取AB=c，作AB的垂直平分线交AB于点O； ② 以点O为圆心，OB长为半径画圆；

③ 以点B为圆心，a长为半径画弧，与⊙O交于点C；④ 连接BC，AC．

则Rt△ABC即为所求．老师说：“小芸的作法正确．”

请回答：小芸的作法中判断∠ACB是直角的依据是________________________．

直径所对的圆周角为直角 【解析】试题分析：根据圆周角定理的推论求解． 【解析】 小芸的作法中判断∠ACB是直角的依据是直径所对的圆周角为直角. 故答案为：直径所对的圆周角为直角.

已知一个正六边形的边心距为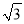，则它的半径为______ ．

2 【解析】试题分析：设正六边形的中心是O，一边是AB，过O作OG⊥AB与G，在直角△OAG中，根据三角函数即可求得OA． 【解析】 如图所示, 在Rt△AOG中,OG=,∠AOG=30°， ∴OA=OG÷cos 30°=÷=2； 故答案为：2.

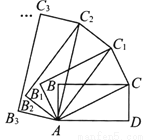
（3分）如图，在矩形ABCD中，AD=2，CD=1，连接AC，以对角线AC为边，按逆时针方向作矩形ABCD的相似矩形AB1C1C，再连接AC1，以对角线AC1为边作矩形AB1C1C的相似矩形AB2C2C1，．．．，按此规律继续下去，则矩形ABnCnCn-1的面积为 ．

（或）． 【解析】 试题分析：AC===，因为矩形都相似，且每相邻两个矩形的相似比=，∴=2×1=2，=，===， ．．．，==．．．===． 故答案为：．