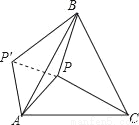
如图，P是正三角形ABC内的一点，且PA=6，PB=8，PC=10，若将△PAC绕点A逆时针旋转后得到△P′AB．

（1）求点P与点P′之间的距离；

（2）求∠APB的大小．

（1）6；（2）150° 【解析】试题分析：先根据等边三角形的性质得AB=AC，∠BAC=60°，再利用旋转的性质得∠P′AP=∠BAC=60°，AP′=AP，BP′=CP=13，于是可判断△AP′P为等边三角形，得到PP′=AP=5，∠APP′=60°，接着根据勾股定理的逆定理证明△BPP′为直角三角形，且∠BPP′=90°，然后利用∠APB=∠APP′+∠BPP′求出∠APB的度数． ...

民间剪纸是中国民间美术形式之一，有着悠久的历史，如图的图案是中心对称图形的是（ ）

D 【解析】 试题分析：根据中心对称图形的概念求解． 【解析】 A、不是中心对称图形．故选项错误； B、不是中心对称图形．故选项错误； C、不是中心对称图形．故选项错误； D、是中心对称图形．故选项正确． 故选D．

已知点P（2+m，n﹣3）与点Q（m，1+n）关于原点对称，则m﹣n的值是（ ）

A．1 B．﹣1 C．2 D．﹣2

D 【解析】 试题分析：根据关于原点对称的点的横坐标互为相反数，纵坐标互为相反数，可得m、n的值，根据有理数的减法，可得答案． 【解析】 由点P（2+m，n﹣3）与点Q（m，1+n）关于原点对称，得 2+m+m=0，n﹣3+1+n=0． 解得m=﹣1，n=1． m﹣n=﹣1﹣1=﹣2， 故选：D．

下列各图中，图形甲变成图形乙，既能用平移，又能用旋转的是(　C　)

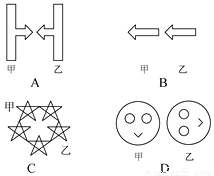
A. A B. B C. C D. D

C 【解析】试题分析：A只能通过旋转180°得到；B只能通过平移得到；D只能通过旋转得到；C能用平移，又能用旋转得到，故选C.

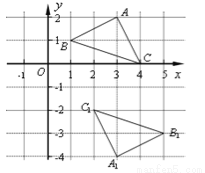
如图，在平面直角坐标系中， 若△ABC与△A1B1C1关于E点成中心对称， 则对称中心E点的坐标是 ．

（3，-1） 【解析】 试题分析：连接对应点AA1、CC1，根据对应点的连线经过对称中心，则交点就是对称中心E点，在坐标系内确定出其坐标． 试题解析：如图： 连接AA1、CC1，则交点就是对称中心E点．观察图形知，E（3，-1）．

已知a＜0，则点P（a2，﹣a+3）关于原点的对称点P1在第_____象限．

三 【解析】本题主要考查了关于原点对称的点的坐标. 根据平面直角坐标系中任意一点P（x，y），关于原点的对称点是（-x，-y），即关于原点的对称点，横纵坐标都变成相反数，求得点P（a2，-a+3）关于原点对称点的坐标是（-a2，a-3），再判定横纵坐标与0的关系，最后即可确定所在的象限． 【解析】 ∵点P（a2，-a+3）关于原点对称点的坐标是（-a2，a-3）， 又∵a＜0，...

在平行四边形、矩形、菱形、正方形、等腰梯形这五种图形中，既是轴对称图形，又是中心对称图形的是_____________．

矩形、菱形、正方形 【解析】本题主要考查了轴对称图形和中心对称图形的概念. 轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合． 根据轴对称图形和中心对称图形的概念作答． 【解析】 两者都是的是矩形，菱形，正方形； 其中平行四边形只是中心对称图形； 等腰梯形只是轴对称图形． 故既是轴对称，又是中心对称的...

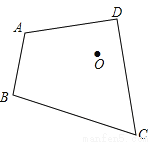
如图，已知四边形ABCD及点O．求作：四边形A′B′C′D′，使得四边形与四边形ABCD关于O点中心对称

作图见解析. 【解析】 试题分析：根据中心对称的性质，连结AO并延长到A′，使OA′=OA，则点A和点A′关于点O对称，同样作出点B、C、D的对应点B′、C′、D′，则四边形A′B′C′D′为满足条件的四边形． 试题解析：如图，四边形A′B′C′D′为所作．

如图所示的正方形网格中，△ABC的顶点均在格点上，请在所给直角坐标系中按要求画图．

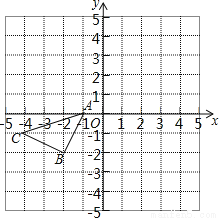
（1）将△ABC向右平移1个单位长度，再向上平移4个单位长度，请画出平移后的△A1B1C1．

（2）画出△ABC关于坐标原点O成中心对称的△A2B2C2．

见解析 【解析】 试题分析：（1）直接利用平移的性质得出各点坐标，进而得出答案； （2）直接利用关于原点对称点的性质得出各点坐标，进而得出答案． 【解析】 （1）如图所示：△A1B1C1，即为所求； （2）如图所示：△A2B2C2，即为所求．

某村原有林地108公顷，旱地54公顷，为保护环境，需把一部分旱地改造为林地，使旱地面积占林地面积的20%．设把x公顷旱地改为林地，则可列方程（ ）

A. 54-x=20%×108 B. 54-x=20%（108+x）

C. 54+x=20%×162 D. 108-x=20%（54+x）

B 【解析】试题解析：设把x公顷旱地改为林地，根据题意可得方程：54-x=20%（108+x）． 故选B．