
科目: 来源:2017-2018学年人教八年级数学上册 第14章 章末综合检测 题型:解答题
(1)先化简,再求值:a(a-2b)+(a+b)2,其中a=-1,b=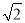 ;
;
(2)若x2-5x=3,求(x-1)(2x-1)-(x+1)2+1的值.
【答案】(1)原式= 2a2+b2=2+2=4;(2)原式=4.
【解析】试题分析:(1)利用完全平方公式展开,化简,代入求值. (2) 利用完全平方公式展开,化简,整体代入求值.
解:(1)原式=a2-2ab+a2+2ab+b2=2a2+b2.
当a=-1,b=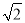 时,原式=2+2=4.
时,原式=2+2=4.
(2)原式=2x2-3x+1-(x2+2x+1)+1=x2-5x+1=3+1=4.
【题型】解答题
【结束】
22
已知化简(x2+px+8)(x2-3x+q)的结果中不含x2项和x3项.
(1)求p,q的值.
(2)x2-2px+3q是否是完全平方式?如果是,请将其分解因式;如果不是,请说明理由.
(1);(2)x2-2px+3q不是完全平方式.理由见解析. 【解析】试题分析:(1)展开,化简,让x2项和x3项系数为0. (2)把(1)中结论代入,不满足完全平方公式. 试题解析: 解:(1)原式=x4+(-3+p)x3+(q-3p+8)x2+(pq-24)x+8q. ∵结果中不含x2项和x3项,∴ 解得 (2)x2-2px+3q不是完全平方式.理由如...查看答案和解析>>
科目: 来源:2017-2018学年人教八年级数学上册 第14章 章末综合检测 题型:解答题
已知化简(x2+px+8)(x2-3x+q)的结果中不含x2项和x3项.
(1)求p,q的值.
(2)x2-2px+3q是否是完全平方式?如果是,请将其分解因式;如果不是,请说明理由.
【答案】(1)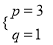 ;(2)x2-2px+3q不是完全平方式.理由见解析.
;(2)x2-2px+3q不是完全平方式.理由见解析.
【解析】试题分析:(1)展开,化简,让x2项和x3项系数为0.
(2)把(1)中结论代入,不满足完全平方公式.
试题解析:
解:(1)原式=x4+(-3+p)x3+(q-3p+8)x2+(pq-24)x+8q.
∵结果中不含x2项和x3项,∴ 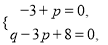
解得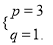
(2)x2-2px+3q不是完全平方式.理由如下:
把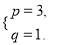 代入x2-2px+3q,得x2-2px+3q=x2-6x+3.
代入x2-2px+3q,得x2-2px+3q=x2-6x+3.
∵x2-6x+9是完全平方式,∴x2-6x+3不是完全平方式.
【题型】解答题
【结束】
23
下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4因式分解的过程.
【解析】
设x2-4x=y,
则原式=(y+2)(y+6)+4(第一步)
=y2+8y+16(第二步)
=(y+4)2(第三步)
=(x2-4x+4)2(第四步)
解答下列问题:
(1)该同学第二步到第三步运用了因式分解的方法是( )
A.提取公因式 B.平方差公式 C.两数和的完全平方公式 D.两数差的完全平方公式
(2)该同学因式分解的结果是否彻底?(填“彻底”或“不彻底”).若不彻底,请直接写出因式分解的最后结果;
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
(1)C;(2)不彻底,(x-2)4;(3)(x-1)4. 【解析】试题分析:(1)从二步到第三步运用了完全平方和公式;(2)x2-4x+4可运用完全平方差公式因式分解;(3)设x2-2x=y,将(x2-2x)(x2-2x+2)+1变形成y(y+2)+1的形式,再进行因式分解; 试题解析: (1)运用了C,两数和的完全平方公式; (2)不彻底; (x2-4x+4)2=...查看答案和解析>>
科目: 来源:2017-2018学年人教八年级数学上册 第14章 章末综合检测 题型:解答题
下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4因式分解的过程.
【解析】
设x2-4x=y,
则原式=(y+2)(y+6)+4(第一步)
=y2+8y+16(第二步)
=(y+4)2(第三步)
=(x2-4x+4)2(第四步)
解答下列问题:
(1)该同学第二步到第三步运用了因式分解的方法是( )
A.提取公因式 B.平方差公式 C.两数和的完全平方公式 D.两数差的完全平方公式
(2)该同学因式分解的结果是否彻底?(填“彻底”或“不彻底”).若不彻底,请直接写出因式分解的最后结果;
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
【答案】(1)C;(2)不彻底,(x-2)4;(3)(x-1)4.
【解析】试题分析:(1)从二步到第三步运用了完全平方和公式;(2)x2-4x+4可运用完全平方差公式因式分解;(3)设x2-2x=y,将(x2-2x)(x2-2x+2)+1变形成y(y+2)+1的形式,再进行因式分解;
试题解析:
(1)运用了C,两数和的完全平方公式;
(2)不彻底;
(x2-4x+4)2=(x-2)4
(3)设x2-2x=y.
(x2-2x)(x2-2x+2)+1
=y(y+2)+1
=y2+2y+1
=(y+1)2…………………………7分
=(x2-2x+1)2
=(x-1)4.
【题型】解答题
【结束】
24
乘法公式的探究及应用.
探究问题
图1是一张长方形纸条,将其剪成长短两条后刚好能拼成图2.


(1) (2)
(1)图1中长方形纸条的面积可表示为_______(写成多项式乘法的形式).
(2)拼成的图2阴影部分的面积可表示为________(写成两数平方差的形式).
(3)比较两图阴影部分的面积,可以得到乘法公式:____.
结论运用
(4)运用所得的公式计算:
 =________;
=________;  =________.
=________.
拓展运用:
(5)计算: 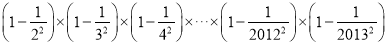
查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.3实际问题与二次函数(3)测试 题型:单选题
抛物线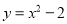 的顶点坐标为( )
的顶点坐标为( )
A. (2,0) B. (-2,0) C. (0,2) D. (0,-2)
D 【解析】试题分析:对于二次函数的顶点坐标为(0,b),根据题意可知二次函数的顶点坐标为(0,-2),故选择D.查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.3实际问题与二次函数(3)测试 题型:单选题
汽车刹车距离s (m)与速度v (km/h)之间的函数关系是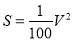 ,一辆车速为100km/h的汽车,刹车距离是 ( )
,一辆车速为100km/h的汽车,刹车距离是 ( )
A. 1m B. 10m C. 100m D. 200 m
C 【解析】试题分析:将V=100代入函数解析式可得:S=m,故选择C.查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.3实际问题与二次函数(3)测试 题型:单选题
如图1,△ABC是直角三角形,∠A=90°,AB=8cm,AC=6cm点P从点A出发,沿AB方向以2cm/s的速度向点B运动;同时点Q从点A出发,沿AC方向以1cm/s的速度向点C运动,其中一个动点到达终点,则另一个动点也停止运动,则三角形APQ的最大面积是( )
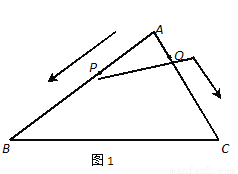
A. 8cm2 B. 16cm2 C. 24cm2 D. 32cm2
B 【解析】试题分析:根据题意可得:AP=2xcm,AQ=xcm,则S=,则根据题意可知:当x=4cm时,面积有最大值,最大面积为16.查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.3实际问题与二次函数(3)测试 题型:单选题
小敏在今年的校运动会跳远比赛中跳出了满意一跳,函数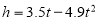 (的单位:秒,
(的单位:秒,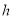 的单位:米)可以描述他跳跃时重心高度的变化,则他起跳后到重心最高时所用的时间是( )
的单位:米)可以描述他跳跃时重心高度的变化,则他起跳后到重心最高时所用的时间是( )
A.0.71s B.0.70s C.0.63s D.0.36s
D 【解析】 试题分析:二次函数可配方成 .当,重心最高.查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.3实际问题与二次函数(3)测试 题型:单选题
心理学家发现,学生对概念的接受能力y与提出概念所用的时间x(单位:分)之间满足函数关系:y=-0.1x2+2.6x+43 (0≤x≤30).
y值越大,表示接受能力越强.如果学生的接受能力逐步增强,则x的取值范围是( )
A. 0≤x≤13 B. 13≤x≤26 C. 0≤x≤26 D. 13≤x≤30
A 【解析】试题分析:对于开口向下的函数而言,对称轴的左边为增函数,对称轴的右边为减函数.本题中二次函数的对称轴为:直线x=13,则当时,y随着x的增大而增大,故选择A.查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.3实际问题与二次函数(3)测试 题型:单选题
图3是某河上一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,抛物线两端点与水面的距离都是1m,拱桥的跨度为10m,桥洞与水面的最大距离是5m,桥洞两侧壁上各有一盏距离水面4m的景观灯.若把拱桥的截面图放在平面直角坐标系中,则两盏景观灯之间的水平距离是( )
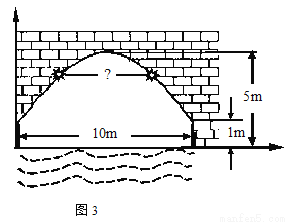
A .3m B.4m C.5m D.6m
C 【解析】试题分析:设距水面1m的水平线为x轴,抛物线两端点中点为原点设立平面直角坐标系, 则抛物线左端点为(-5,0),右端点为(5,0),顶点为(0,4), 设抛物线为: ,将(5,0)代入可得函数解析式为: ; 将y=3代入函数解析式可得: ,则两盏景观灯之间的水平距离为5m,故选择C.查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.3实际问题与二次函数(3)测试 题型:填空题
二次函数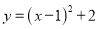 的最小值是____。
的最小值是____。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com