
科目: 来源:贵州省六盘水市2018届九年级上学期第二次月考数学试卷 题型:填空题
若关于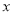 的一元二次方程
的一元二次方程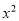 +x-3m=0有两个不相等的实数根,则
+x-3m=0有两个不相等的实数根,则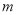 的取值范围是( )
的取值范围是( )
A. 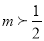 B.
B. 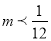 C.
C. 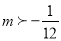 D.
D. 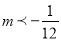
【答案】C
【解析】试题分析:∵a=1,b=1,c=-3m,∴△=b2-4ac=12-4×1×(-3m)=1+12m>0,解得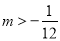 .
.
考点:根的判别式.
【题型】单选题
【结束】
11
若一元二次方程x2-x-1=0的两根分别为x1,x2,则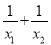 = .
= .
查看答案和解析>>
科目: 来源:贵州省六盘水市2018届九年级上学期第二次月考数学试卷 题型:填空题
若一元二次方程x2-x-1=0的两根分别为x1,x2,则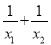 = .
= .
【答案】-1
【解析】∵一元二次方程: 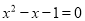 的两根是
的两根是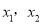 ,
,
∴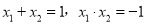 ,
,
∴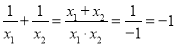 .
.
点睛:不解方程,求含有一元二次方程两根的代数式的值时,通常分两步完成:(1)由方程得到: 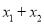 、
、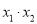 的值(前提是“根的判别式△
的值(前提是“根的判别式△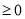 ”);(2)把要求值的代数式变形为用含“
”);(2)把要求值的代数式变形为用含“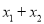 ”和“
”和“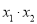 ”表达的形式,再代值计算即可.
”表达的形式,再代值计算即可.
【题型】填空题
【结束】
12
已知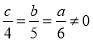 ,则
,则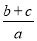 的值为 .
的值为 .
查看答案和解析>>
科目: 来源:贵州省六盘水市2018届九年级上学期第二次月考数学试卷 题型:填空题
已知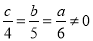 ,则
,则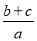 的值为 .
的值为 .
【答案】1.5
【解析】设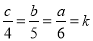 ,则
,则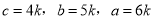 ,
,
∴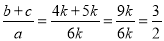 .
.
【题型】填空题
【结束】
13
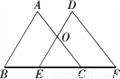
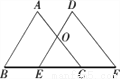
如图,△ABC经过平移到△DEF位置,它们的重叠部分的面积是△ABC的一半,若BC=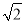 ,则BE= .
,则BE= .
查看答案和解析>>
科目: 来源:贵州省六盘水市2018届九年级上学期第二次月考数学试卷 题型:填空题
如图,△ABC经过平移到△DEF位置,它们的重叠部分的面积是△ABC的一半,若BC=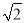 ,则BE= .
,则BE= .
【答案】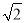 -1.
-1.
【解析】由题意可知:OE∥AB,
∴△OEC∽△ABC,
∴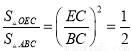 ,即
,即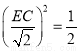 ,解得:EC=1.
,解得:EC=1.
∴BE=BC-EC=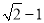 .
.
【题型】填空题
【结束】
14
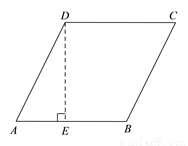
菱形的周长为16,两邻角度数的比为1:2,此菱形的面积为 .
8 . 【解析】如图,由题意可知,在菱形ABCD中,∠A+∠ADC=180°,∠A:∠ADC=1:2,AD=AB=, ∴∠A=60°, 过点D作DE⊥AB于点E,则∠DEA=90°, ∴∠ADE=30°, ∴AE=AD=2, ∴DE=, ∴S菱形ABCD=ABDE=.查看答案和解析>>
科目: 来源:贵州省六盘水市2018届九年级上学期第二次月考数学试卷 题型:填空题
菱形的周长为16,两邻角度数的比为1:2,此菱形的面积为 .
【答案】8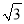 .
.
【解析】如图,由题意可知,在菱形ABCD中,∠A+∠ADC=180°,∠A:∠ADC=1:2,AD=AB=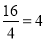 ,
,
∴∠A=60°,
过点D作DE⊥AB于点E,则∠DEA=90°,
∴∠ADE=30°,
∴AE=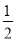 AD=2,
AD=2,
∴DE=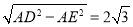 ,
,
∴S菱形ABCD=AB DE=
DE=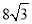 .
.
【题型】填空题
【结束】
15
为了估计湖里游多少条鱼,有下列方案:从湖里捕上100条做上标记,然后放回湖里去,经过一段时间,待带标记的鱼完全混合于鱼群后,第二次再捕上200条,若其中带标记的鱼有25条,那么你估计湖里大约有 条鱼.
800 【解析】试题分析:设湖里有鱼x条,由题意得,100÷x=25÷200,解得x=800,所以可以估算湖里有鱼800条. 故答案为:800.查看答案和解析>>
科目: 来源:贵州省六盘水市2018届九年级上学期第二次月考数学试卷 题型:填空题
为了估计湖里游多少条鱼,有下列方案:从湖里捕上100条做上标记,然后放回湖里去,经过一段时间,待带标记的鱼完全混合于鱼群后,第二次再捕上200条,若其中带标记的鱼有25条,那么你估计湖里大约有 条鱼.
【答案】800
【解析】试题分析:设湖里有鱼x条,由题意得,100÷x=25÷200,解得x=800,所以可以估算湖里有鱼800条.
故答案为:800.
考点:一元一次方程的应用.
【题型】填空题
【结束】
16
如图,在一块长为22 m,宽为17 m的矩形地面上,要修建同样宽的两条互相垂直的道路(两条道路各与矩形的一条边平行),剩余部分种上草坪,使草坪面积为300 m2.若设道路宽为x m,根据题意可列出方程为______________________________.

查看答案和解析>>
科目: 来源:贵州省六盘水市2018届九年级上学期第二次月考数学试卷 题型:填空题
如图,在一块长为22 m,宽为17 m的矩形地面上,要修建同样宽的两条互相垂直的道路(两条道路各与矩形的一条边平行),剩余部分种上草坪,使草坪面积为300 m2.若设道路宽为x m,根据题意可列出方程为______________________________.

【答案】(22-x)(17-x)=300(或x2-39x+74=0)
【解析】试题分析:把所修的两条道路分别平移到矩形的最上边和最左边,则剩下的草坪是一个长方形,根据长方形的面积公式列方程.设道路的宽应为x米,由题意有(22﹣x)(17﹣x)=300,故答案为:(22﹣x)(17﹣x)=300.
考点:由实际问题抽象出一元二次方程.
【题型】填空题
【结束】
17
x=1是关于x的一元二次方程x2+mx﹣5=0的一个根,则此方程的另一个根是 .
-5 【解析】把代入方程得: ,解得: , ∴原方程为: ,解此方程得: , ∴此方程的另一根为: .查看答案和解析>>
科目: 来源:贵州省六盘水市2018届九年级上学期第二次月考数学试卷 题型:填空题
x=1是关于x的一元二次方程x2+mx﹣5=0的一个根,则此方程的另一个根是 .
【答案】-5
【解析】把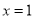 代入方程
代入方程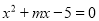 得:
得: 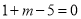 ,解得:
,解得: 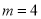 ,
,
∴原方程为: 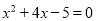 ,解此方程得:
,解此方程得: 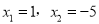 ,
,
∴此方程的另一根为: 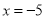 .
.
【题型】填空题
【结束】
18
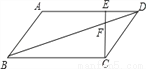
如图,在 ABCD中,E为线段AD上一点,AE=4ED,CE、BD交于点F,若DF=4cm,则BF的长为 .
ABCD中,E为线段AD上一点,AE=4ED,CE、BD交于点F,若DF=4cm,则BF的长为 .
查看答案和解析>>
科目: 来源:贵州省六盘水市2018届九年级上学期第二次月考数学试卷 题型:解答题
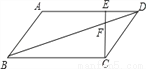
如图,在 ABCD中,E为线段AD上一点,AE=4ED,CE、BD交于点F,若DF=4cm,则BF的长为 .
ABCD中,E为线段AD上一点,AE=4ED,CE、BD交于点F,若DF=4cm,则BF的长为 .
【答案】20
【解析】∵四边形ABCD是平行四边形,AE=4ED,
∴BC=AD=AE+ED=5ED,AD∥BC,
∴△DEF∽△BCF,
∴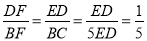 ,即
,即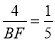 ,
,
∴BF=20.
【题型】填空题
【结束】
19
解方程:(1) 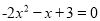 ; (2)
; (2)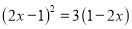 .
.
查看答案和解析>>
科目: 来源:贵州省六盘水市2018届九年级上学期第二次月考数学试卷 题型:解答题
解方程:(1) 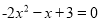 ; (2)
; (2)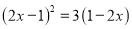 .
.
【答案】(1)x1 =1 ,x2=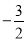 ; (2) x1 =-1,x2=
; (2) x1 =-1,x2=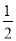 .
.
【解析】试题分析:
根据两方程的特点,使用“因式分解法”解两方程即可.
试题解析:
(1)原方程可化为: 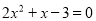 ,
,
方程左边分解因式得: 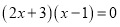 ,
,
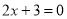 或
或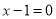 ,
,
解得: 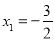 ,
, 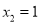 .
.
(2)原方程可化为: 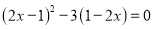 ,即
,即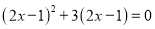 ,
,
∴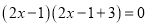 ,
,
∴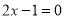 或
或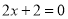 ,
,
解得: 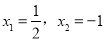 .
.
【题型】解答题
【结束】
20
已知x1,x2是关于x的一元二次方程x2-2(m+1)x+m2+5=0的两实根.
(1)若(x1-1)(x2-1)=28,求m的值;
(2)已知等腰△ABC的一边长为7,若x1,x2恰好是△ABC另外两边的边长,求这个三角形的周长.
(1)m的值为6;(2)17. 【解析】试题分析: (1)由题意和根与系数的关系可得:x1+x2=2(m+1),x1x2=m2+5;由(x1-1)(x2-1)=28,可得:x1x2-(x1+x2)=27;从而得到:m2+5-2(m+1)=27,解方程求得m的值,再由“一元二次方程根的判别式”进行检验即可得到m的值; (2)①当7为腰长时,则方程的两根中有一根为7,代入方程可解得m...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com