
科目: 来源:2017-2018学年度鲍沟中学北师大版八年级数学上册 第一章 勾股定理 检测题 题型:解答题
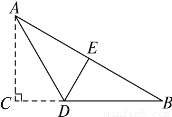
如图,有一块直角三角形纸片,两直角边AC=6 cm,BC=8 cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求CD的长.
查看答案和解析>>
科目: 来源:2017-2018学年度鲍沟中学北师大版八年级数学上册 第一章 勾股定理 检测题 题型:解答题
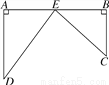
如图,铁路上A,B两点相距25km,C,D为两村庄,AD⊥AB于点A,BC⊥AB于点B,已知AD=15km,BC=10km,现在要在铁路AB旁建一个货运站E,使得C,D两村到E站距离相等,问E站应建在离A地多远的地方?
查看答案和解析>>
科目: 来源:2017-2018学年度鲍沟中学北师大版八年级数学上册 第一章 勾股定理 检测题 题型:解答题
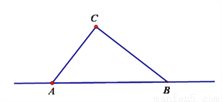
台风是一种自然灾害,它以台风中心为圆心在周围上千米的范围内形成极端气候,有极强的破坏力。如图,有一台风中心沿东西方向AB由点A行驶向点B,已知点 C为一海港,且点 C与直线 AB上两点A,B的距离分别为300km和400km,又 AB=500km,以台风中心为圆心周围250km以内为受影响区域。
(1)海港C受台风影响吗?为什么?
(2)若台风的速度为20km/h,台风影响该海港持续的时间有多长?
(1)海港C受台风影响.理由见解析.(2) 7小时. 【解析】试题分析:(1)利用勾股定理的逆定理得出△ABC是直角三角形,进而利用三角形面积得出CD的长,进而得出海港C是否受台风影响; (2)利用勾股定理得出ED以及EF的长,进而得出台风影响该海港持续的时间; 试题解析: (1)海港C受台风影响。 理由:如图,过点C作CD⊥AB于D, ∵AC=300km,BC=4...查看答案和解析>>
科目: 来源:2017-2018学年度鲍沟中学北师大版八年级数学上册 第一章 勾股定理 检测题 题型:解答题
如图,方格纸中小正方形的边长为1,△ABC的三个顶点都在小正方形的格点上,求:
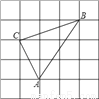
(1) △ABC的面积;
(2)边AC的长;
(3)点B到AC边的距离.
(6分)解(1);(2);(3)h=. 【解析】试题分析:(1)利用三角形所在的正方形面积减三个小直角三角形的面积即可求出; (2)利用勾股定理即可求出AC的长; (3)求出AC,则点B到AC边的距离即为AC边上的高,利用面积公式即可求出. 试题解析:(1)S△ABC=3×3-(×3×1+×2×1+×2×3)=; (2)AC=; (3)设点B到AC边的距离为h,...查看答案和解析>>
科目: 来源:2017-2018学年度鲍沟中学北师大版八年级数学上册 第一章 勾股定理 检测题 题型:解答题
“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过70km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪A处的正前方30m的C处,过了2s后,测得小汽车与车速检测仪间距离为50m,这辆小汽车超速了吗?(参考数据转换:1m/s=3.6km/h)
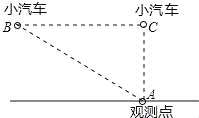
查看答案和解析>>
科目: 来源:安徽省合肥市西校2018届九年级上学期期中考试数学试卷 题型:单选题
抛物线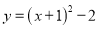 的对称轴是直线( )
的对称轴是直线( )
A. x=-2 B. x=-1 C. x=2 D. x=1
B 【解析】令 解得x=-1,故选B.查看答案和解析>>
科目: 来源:安徽省合肥市西校2018届九年级上学期期中考试数学试卷 题型:单选题
将抛物线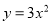 分别向下、向右平移1个单位,所得抛物线的解析式为( )
分别向下、向右平移1个单位,所得抛物线的解析式为( )
A. 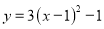 B.
B. 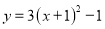
C. 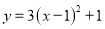 D.
D. 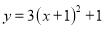
查看答案和解析>>
科目: 来源:安徽省合肥市西校2018届九年级上学期期中考试数学试卷 题型:单选题
若△ABC∽△A′B′C′,相似比为1∶2,则△ABC与△A′B′C′的面积的比为( )
A. 1∶2 B. 2∶1 C. 1∶4 D. 4∶1
C 【解析】试题分析:根据相似三角形面积的比等于相似比的平方计算即可得解.∵△ABC∽△A′B′C′,相似比为1:2,∴△ABC与△A′B′C′的面积的比为1:4. 故选:C.查看答案和解析>>
科目: 来源:安徽省合肥市西校2018届九年级上学期期中考试数学试卷 题型:单选题
如图,在长为8 cm、宽为4 cm的矩形中,截去一个矩形,使得留下的矩形(图中阴影部分)与原矩形相似,则留下矩形的面积是( )
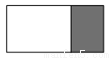
A. 2 cm2 B. 4 cm2 C. 8 cm2 D. 16 cm2
C 【解析】设留下的矩形的宽为x,∵留下的矩形与矩形相似,∴,x=2, ∴留下的矩形的面积为:2×4=8(cm2).故选C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com