
科目: 来源:人教版九年级上册数学 22.3实际问题与二次函数(1)练习 题型:单选题
用长8 m的铝合金条制成使窗户的透光面积最大的矩形窗框(如图),那么这个窗户的最大透光面积是( )

A. 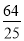 m2 B.
m2 B. 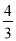 m2 C.
m2 C. 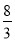 m2 D. 4m2
m2 D. 4m2
查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.3实际问题与二次函数(1)练习 题型:单选题
如图,边长分别为1和2的两个等边三角形,开始它们在左边重合,大三角形固定不动,然后把小三角形自左向右平移直至移出大三角形外停止.设小三角形移动的距离为x,两个三角形重叠面积为y,则y关于x的函数图象是( )
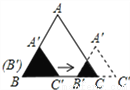
A. 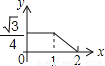 B.
B. 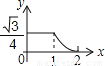
C. 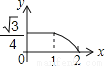 D.
D. 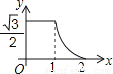
查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.3实际问题与二次函数(1)练习 题型:填空题
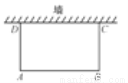
如图,利用一面墙(墙的长度不超过45 m),用80 m长的篱笆围一个矩形场地.当AD=______ m时,矩形场地的面积最大,最大值为______.
查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.3实际问题与二次函数(1)练习 题型:填空题
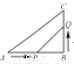
如图,在△ABC中,∠B=90°,AB=8 cm,BC=6 cm,点P从点A开始沿AB向B点以2 cm/s的速度移动,点Q从点B开始沿BC向C点以1 cm/s的速度移动,如果P,Q分别从A,B同时出发,当△PBQ的面积为最大时,运动时间t为______s.
查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.3实际问题与二次函数(1)练习 题型:填空题
将一根长为20 cm的铁丝剪成两段,并以每一段铁丝的长度为周长各做成一个正方形,则这两个正方形面积之和的最小值是______cm2.
cm2 【解析】试题分析:设一段铁丝的长度为x,另一段为(20﹣x),则边长分别为, (20﹣x),则S==,∴由函数当x=10cm时,S最小,为12.5cm2.故答案为:12.5.查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.3实际问题与二次函数(1)练习 题型:解答题
某高中学校为高一新生设计的学生单人桌的抽屉部分是长方体形.其中,抽屉底面周长为180cm,高为20cm.请通过计算说明,当底面的宽x为何值时,抽屉的体积y最大?最大为多少?(材质及其厚度等暂忽略不计).
当抽屉底面宽为45cm时,抽屉的体积最大,最大体积为40500cm3 【解析】【解析】 已知抽屉底面宽为x cm,则底面长为180÷2-x=(90-x)cm. 由题意得:。 ∴当x=45时,y有最大值,最大值为40500。 答:当抽屉底面宽为45cm时,抽屉的体积最大,最大体积为40500cm3。 根据题意列出二次函数关系式,然后利用二次函数的性质求最大值。 ...查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.3实际问题与二次函数(1)练习 题型:填空题
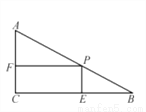
如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=12cm,点P是AB边上的一个动点,过点P作PE⊥BC于点E,PF⊥AC于点F,当PB=6cm时,四边形PECF的面积最大,最大值为______
查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.3实际问题与二次函数(1)练习 题型:解答题
在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.
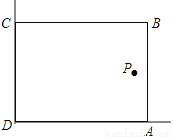
(1)若花园的面积为192m2,求x的值;
(2)若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求x取何值时,花园面积S最大,并求出花园面积S的最大值.
(1)x的值为12或16;(2)花园面积S的最大值为195平方米. 【解析】试题分析:(1)根据题意得出长×宽=192,进而得出答案; (2)由题意可得出:S=x(28-x)=-x2+28x=-(x-14)2+196,再利用二次函数增减性求得最值. 试题解析:(1)∵AB=x,则BC=(28-x), ∴x(28-x)=192, 解得:x1=12,x2=16, 答...查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.3实际问题与二次函数(1)练习 题型:解答题
手工课上,小明准备做一个形状是菱形的风筝,这个菱形的两条对角线长度之和恰好为60 cm,菱形的面积S(单位:cm2)随其中一条对角线的长x(单位:cm)的变化而变化.
(1)请直接写出S与x之间的函数关系式(不要求写出自变量x的取值范围);
(2)当x是多少时,菱形风筝面积S最大?最大面积是多少?
(1) (2) 450cm2 【解析】试题分析:已知其中一条对角线的长x,则另一对角线=60-x。所以S=x(60-x),整理得。(2)由(1)知菱形风筝面积S图像为关于x的一个二次函数图像,开口向下的抛物线,S最大值为顶点坐标时。根据当x=-时,二次函数y=ax2+bx+c(a≠0)有最小(大)值,所以时,查看答案和解析>>
科目: 来源:人教版九年级上册数学 22.3实际问题与二次函数(1)练习 题型:解答题
用长为32米的篱笆围一个矩形养鸡场,设围成的矩形一边长为x米,面积为y平方米.
(1)求y关于x的函数解析式;
(2)当x为何值时,围成的养鸡场面积为60平方米?
(3)能否围成面积为70平方米的养鸡场?如果能,请求出其边长;如果不能,请说明理由.
(1)y关于x的函数解析式是y=-x2+16x; (2)当x是6或10时,围成的养鸡场面积为60平方米; (3)不能围成面积为70平方米的养鸡场.理由见解析. 【解析】试题分析:(1)根据矩形的面积公式进行列式; (2)、(3)把y的值代入(1)中的函数关系,求得相应的x值即可. 【解析】 (1)设围成的矩形一边长为x米,则矩形的邻边长为:32÷2﹣x.依题意得 ...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com