
科目: 来源:人教版九年级上册数学 24.2.2直线和圆的位置关系(3)练习 题型:填空题
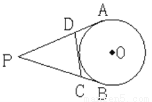
如图,PA、PB分别切圆O于A、B两点,并与圆O的切线分别相交于C、D两点,已知PA=7cm,则△PCD的周长等于_________.
查看答案和解析>>
科目: 来源:人教版九年级上册数学 24.2.2直线和圆的位置关系(3)练习 题型:单选题
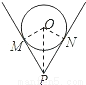
一个钢管放在V形架内,如图是其截面图,O为钢管的圆心.如果钢管的半径为25cm,∠MPN=60°,则OP=( )
A.50cm B.25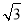 cm C.
cm C.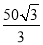 cm D.50
cm D.50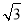 cm
cm
查看答案和解析>>
科目: 来源:人教版九年级上册数学 24.2.2直线和圆的位置关系(3)练习 题型:解答题
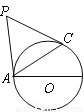
如图,已知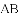
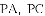
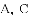
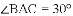
(1)求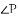
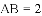
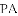
查看答案和解析>>
科目: 来源:人教版九年级上册数学 24.2.2直线和圆的位置关系(3)练习 题型:解答题
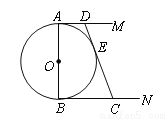
如图,⊙O 的直径AB=2,AM和BN是它的两条切线,DE切⊙O于E,交AM于D,交BN于C.设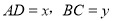 .
.
(1)求证: 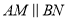 ;(2)求
;(2)求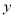 关于
关于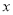 的关系式.
的关系式.
查看答案和解析>>
科目: 来源:人教版九年级上册数学 24.2.2直线和圆的位置关系(3)练习 题型:填空题
如图,PA、PB分别切⊙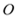 于点A、B,点E是⊙O上一点,且
于点A、B,点E是⊙O上一点,且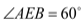 ,则
,则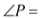 _______度.
_______度.
查看答案和解析>>
科目: 来源:人教版九年级上册数学 24.2.2直线和圆的位置关系(3)练习 题型:填空题
如图,边长为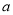 的正三角形的内切圆半径是_________.
的正三角形的内切圆半径是_________.

查看答案和解析>>
科目: 来源:人教版九年级上册数学 24.2.2直线和圆的位置关系(3)练习 题型:解答题
如图,AB是 的的直径,BC
的的直径,BC AB于点B,连接OC交
AB于点B,连接OC交 于点E,弦AD//OC,弦DF
于点E,弦AD//OC,弦DF AB于点G.
AB于点G.
(1)求证:点E是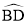 的中点;
的中点;
(2)求证:CD是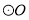 的切线;
的切线;
查看答案和解析>>
科目: 来源:人教版九年级上册数学 24.2.2直线和圆的位置关系(3)练习 题型:解答题
已知:如图,在 △ABC中,∠ABC=90°,以AB上的点O为圆心,OB的长为半径的圆与AB交于点E,与AC切于点D.
△ABC中,∠ABC=90°,以AB上的点O为圆心,OB的长为半径的圆与AB交于点E,与AC切于点D.
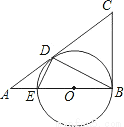
(1)求证:BC=CD;
(2)求证:∠ADE=∠ABD;
(1)证明见解析;(2)证明见解析. 【解析】 试题分析:从切线的性质出发,通过切线与弦所夹的角与弧弦夹角相等,即得到∠CDB=∠CBA;由切线的性质而求得. 试题解析:(1)证明:∵∠ABC=90°, ∴OB⊥BC ∵OB是⊙O的半径, ∴CB为⊙O的切线. 又∵CD切⊙O于点D, ∴BC=CD; (2)证明:∵BE是⊙O的直径, ∴∠...查看答案和解析>>
科目: 来源:人教版九年级上册数学 24.2.2直线和圆的位置关系(3)练习 题型:解答题
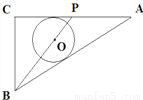
如图,△ABC中,∠C=90°,AC=8cm,AB=10cm,点P由点C出发以每秒2cm的速度沿CA向点A运动(不运动至A点),⊙O的圆心在BP上,且⊙O分别与AB、AC相切,当点P运动2秒钟时,求⊙O的半径.
查看答案和解析>>
科目: 来源:人教版九年级上册数学 24.2.2直线和圆的位置关系(3)练习 题型:填空题
如图,PA、PB分别与⊙O相切于点A、B,⊙O的切线EF分别交PA、PB于点E、F,切点C在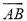 上,若PA长为2,则△PEF的周长是 .
上,若PA长为2,则△PEF的周长是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com