
科目: 来源:江苏省2018届九年级12月月考数学试卷 题型:填空题
二次函数y=x2﹣2x+6的最小值是____.
5 【解析】试题分析:y=x2﹣2x+6=x2﹣2x+1+5 =(x﹣1)2+5, 可见,二次函数的最小值为5.查看答案和解析>>
科目: 来源:江苏省2018届九年级12月月考数学试卷 题型:解答题
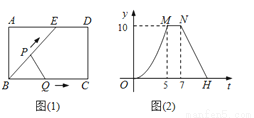
如图(1),E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P沿折线BE-ED-DC运动到点C时停止,点Q沿BC运动到点C时停止,运动的速度都是1cm/秒.设P、Q同发t秒时,△BPQ的面积为ycm2.已知y与t的函数关系图象如图(2)(曲线OM为抛物线的一部分),则下列结论:①AD=BE=5;②cos∠ABE=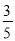 ;③当0<t≤5时,y=
;③当0<t≤5时,y=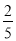 t2;④当t=
t2;④当t=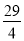 秒时,△ABE∽△QBP;其中正确的结论是______(填序号).
秒时,△ABE∽△QBP;其中正确的结论是______(填序号).
查看答案和解析>>
科目: 来源:江苏省2018届九年级12月月考数学试卷 题型:解答题
(1)解方程: 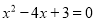 ;
;
(2)计算: 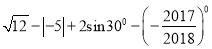 .
.
查看答案和解析>>
科目: 来源:江苏省2018届九年级12月月考数学试卷 题型:解答题
一个不透明的布袋里装有2个白球,1个黑球和若干个红球,它们除颜色外其余都相同.从中任意摸出1个球,取出白球的概率为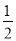 .
.
(1)布袋里红球有 个;
(2)先从布袋中摸出1个球后不再放回,再摸出1个球,求两次摸到的球都是白球的概率.
(1)1;(2). 【解析】试题分析:(1)设红球的个数为x,根据白球的概率可得关于x的方程,解方程即可; (2)画出树形图,即可求出两次摸到的球都是白球的概率. 试题解析:(1)设红球的个数为x,由题意可得: , 解得:x=1,经检验x=1是方程的根, 即红球的个数为1个; (2)画树状图如下: ∴P(摸得两白)=.查看答案和解析>>
科目: 来源:江苏省2018届九年级12月月考数学试卷 题型:解答题
已知抛物线的顶点为(1,﹣4),且过点(﹣2,5).
(1)求抛物线解析式;
(2)求函数值y>0时,自变量x的取值范围.
(1)y=x2﹣2x﹣3;(2)x<﹣1或x>3时,y>0. 【解析】试题分析:(1)由于已知抛物线顶点坐标,则可设顶点式y=a(x﹣1)2﹣4,然后把(﹣2,5)代入求出a的值即可; (2)先求出抛物线与x轴的交点坐标,然后写出抛物线在x轴上方所对应的自变量的取值范围即可. 【解析】 (1)设抛物线解析式为y=a(x﹣1)2﹣4, 把(﹣2,5)代入得a•(﹣2﹣1)2...查看答案和解析>>
科目: 来源:江苏省2018届九年级12月月考数学试卷 题型:解答题
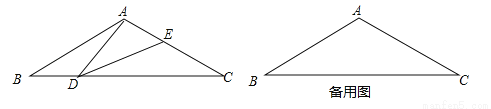
如图,在等腰三角形ABC中,∠BAC=120°,AB=AC=2,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=30°.
(1)求证:△ABD∽△DCE;
(2)设BD=x,AE=y,求y关于x的函数关系式并写出自变量x的取值范围.
查看答案和解析>>
科目: 来源:江苏省2018届九年级12月月考数学试卷 题型:解答题
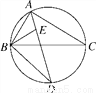
如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E.
(1)求证:DE=DB;
(2)若∠BAC=90°,BD=4,求△ABC外接圆的半径.
查看答案和解析>>
科目: 来源:江苏省2018届九年级12月月考数学试卷 题型:解答题
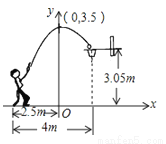
如图所示,一位运动员在距篮下4米处跳起投篮,球运行的路线是抛物线,当球运行的水平距离为2.5m时,达到最大高度3.5m,然后准确落入篮圈.已知篮圈中心到地面的距离为3.05m.
(1)建立如图所示的直角坐标系,求抛物线的解析式;
(2)该运动员身高1.8m,在这次跳投中,球在头顶上方0.25m处出手,问:球出手时,他跳离地面的高度是多少?
查看答案和解析>>
科目: 来源:江苏省2018届九年级12月月考数学试卷 题型:解答题
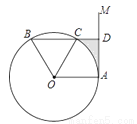
如图,点A是直线AM与⊙O的交点,点B在⊙O上,BD⊥AM垂足为D,BD与⊙O交于点C,OC平分∠AOB,∠B=60°.
(1)求证:AM是⊙O的切线;
(2)若DC=2,求图中阴影部分的面积.(结果保留π和根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com