
科目: 来源:郑州二中学区2017-2018学年上学期期中学业水平测试 八年级数学试卷 题型:解答题
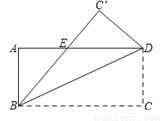
如图,将长方形ABCD沿对角线BD折叠,使点C落在C′处,BC′交AD于点E.
(1)试判断△BDE的形状,并说明理由;
(2)若AB=4,AD=8,求△BDE的面积.
【答案】(1)△BDE是等腰三角形;(2)10.
【解析】试题分析:(1)由折叠可知,∠CBD=∠EBD,再由AD∥BC,得到∠CBD=∠EDB,即可得到∠EBD=∠EDB,于是得到BE=DE,等腰三角形即可证明;
(2)设DE=x,则BE=x,AE=8﹣x,在Rt△ABE中,由勾股定理求出x的值,再由三角形的面积公式求出面积的值.
【解析】
(1)△BDE是等腰三角形.
由折叠可知,∠CBD=∠EBD,
∵AD∥BC,
∴∠CBD=∠EDB,
∴∠EBD=∠EDB,
∴BE=DE,
即△BDE是等腰三角形;
(2)设DE=x,则BE=x,AE=8﹣x,
在Rt△ABE中,由勾股定理得:AB2+AE2=BE2即42+(8﹣x)2=x2,
解得:x=5,
所以S△BDE= DE×AB=
DE×AB= ×5×4=10.
×5×4=10.
考点:翻折变换(折叠问题).
【题型】解答题
【结束】
18
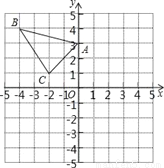
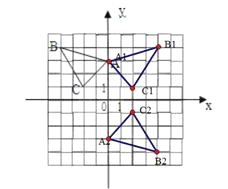
△ABC在直角坐标系内的位置如图所示.
(1)分别写出A、B、C的坐标;
(2)请在这个坐标系内画出△A1B1C1,使△A1B1C1与△ABC关于y轴对称,并写出B1的坐标;
(3)请在这个坐标系内画出△A2B2C2,使△A2B2C2与△ABC关于原点对称,并写出A2的坐标.
查看答案和解析>>
科目: 来源:郑州二中学区2017-2018学年上学期期中学业水平测试 八年级数学试卷 题型:解答题
△ABC在直角坐标系内的位置如图所示.
(1)分别写出A、B、C的坐标;
(2)请在这个坐标系内画出△A1B1C1,使△A1B1C1与△ABC关于y轴对称,并写出B1的坐标;
(3)请在这个坐标系内画出△A2B2C2,使△A2B2C2与△ABC关于原点对称,并写出A2的坐标.
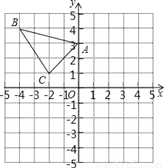
【答案】(1)A(0,3);B(﹣4,4);C(﹣2,1);(2)B1的坐标为:(4,4);(3)A2(0,﹣3)
【解析】试题分析:(1)根据三角形在平面直角坐标系的位置,分别写出作标点;(2)作关于y轴对称的图形见解析;(3)作关于原点对称图形见解析;
试题解析:(1)根据平面直角坐标系可知点A,B,C的坐标为A(0,3);B(-4,4);C(-2,1);
(2)作图如下图: (4,4);(3)作图如下:
(4,4);(3)作图如下: (0,-3).
(0,-3).
考点:1.作图-轴对称变换2.作图-中心对称变换3.象限内点的坐标
【题型】解答题
【结束】
19
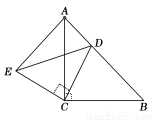
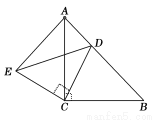
如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点,求证:
(1)△ACE≌△BCD;(2)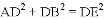 .
.
查看答案和解析>>
科目: 来源:郑州二中学区2017-2018学年上学期期中学业水平测试 八年级数学试卷 题型:解答题
如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点,求证:
(1)△ACE≌△BCD;(2)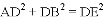 .
.
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)本题要判定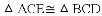
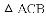
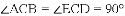
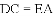
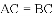

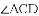

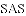
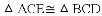
(2)由(1)的论证结果得出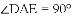
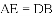
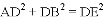 .
.
试题解析:
(1)∵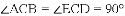
∴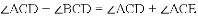
∴
∵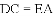
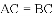
∴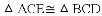
(2)∵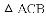
∴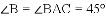
∵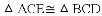
∴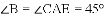
∴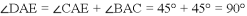
∴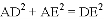 .
.
由(1)知AE=DB,
∴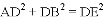 .
.
考点:(1)勾股定理;(2)全等三角形的判定与性质;(3)等腰直角三角形.
【题型】解答题
【结束】
20
已知一次函数y=2x+4
(1)在如图所示的平面直角坐标系中,画出函数的图象;
(2)求图象与x轴的交点A的坐标,与y轴交点B的坐标;
(3)在(2)的条件下,求出△AOB的面积;
(4)利用图象直接写出:当y<0时,x的取值范围.
查看答案和解析>>
科目: 来源:郑州二中学区2017-2018学年上学期期中学业水平测试 八年级数学试卷 题型:解答题
已知一次函数y=2x+4
(1)在如图所示的平面直角坐标系中,画出函数的图象;
(2)求图象与x轴的交点A的坐标,与y轴交点B的坐标;
(3)在(2)的条件下,求出△AOB的面积;
(4)利用图象直接写出:当y<0时,x的取值范围.
【答案】(1)画图见解析;(2)A(﹣2,0)B(0,4);(3)4;(4)x<﹣2.
【解析】试题分析:(1)求得一次函数y=2x+4与x轴、y轴的交点坐标,利用两点确定一条直线就可以画出函数图象;(2)由(1)即可得结论;(3)通过交点坐标根据三角形的面积公式即可求出面积;(4)观察函数图象与x轴的交点就可以得出结论.
试题解析:(1)当x=0时y=4,当y=0时,x=﹣2,则图象如图所示
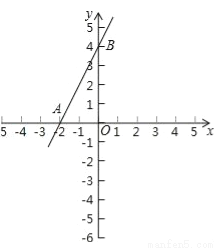
(2)由上题可知A(﹣2,0)B(0,4),
(3)S△AOB=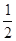 ×2×4=4,
×2×4=4,
(4)x<﹣2.
考点:一次函数图象与系数的关系;一次函数的图象.
【题型】解答题
【结束】
21
在社会主义新农村建设中,衢州某乡镇决定对A、B两村之间的公路进行改造,并有甲工程队从A村向B村方向修筑,乙工程队从B村向A村方向修筑.已知甲工程队先施工3天,乙工程队再开始施工.乙工程队施工几天后因另有任务提前离开,余下的任务有甲工程队单独完成,直到公路修通.下图是甲乙两个工程队修公路的长度y(米)与施工时间x(天)之间的函数图象,请根据图象所提供的信息解答下列问题:
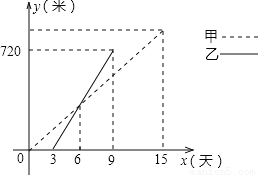
(1)乙工程队每天修公路多少米?
(2)分别求甲、乙工程队修公路的长度y(米)与施工时间x(天)之间的函数关系式.
(3)若该项工程由甲、乙两工程队一直合作施工,需几天完成?
(1)乙工程队每天修公路120米;(2)y甲=60x,y乙=120x-360;(3)该项工程由甲、乙两工程队一直合作施工,需9天完成. 【解析】试题分析:(1)根据图象得出乙每天修的米数;(2)根据待定系数法求出函数解析式;(3)首先求出总的路程,然后计算. 试题解析:(1)∵720÷(9-3)=120∴乙工程队每天修公路120米. (2)设y乙=kx+b,则∴∴y乙=120x-...查看答案和解析>>
科目: 来源:人教版九年级上册数学 21.3实际问题与一元二次方程(1) 测试 题型:单选题
今年以来,某种食品不断上涨,在9月份的售价为8.1元/kg,11月份的售价为10元/kg。这种食品平均每月上涨的百分率约等于( ).
A. 15℅ B. 11℅ C. 20℅ D. 9℅
B 【解析】试题分析:10月份的售价=9月份的售价×(1+增长率),11月份的售价=10月份的售价×(1+增长率),把相关数值代入后化简即可.设这种食品平均每月上涨的百分率为x,根据题意得:8.1(1+x)2=10, 解得:x1≈0.11,x2≈-1.11(舍去)查看答案和解析>>
科目: 来源:人教版九年级上册数学 21.3实际问题与一元二次方程(1) 测试 题型:单选题
六一儿童节当天,某班同学每人向本班其他每个同学送一份小礼品,全班共互送1035份小礼品,如果全班有x名同学,根据题意列出方程为( )
A. 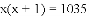
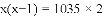
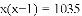
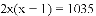
查看答案和解析>>
科目: 来源:人教版九年级上册数学 21.3实际问题与一元二次方程(1) 测试 题型:单选题
为执行“二免一补”政策,某地区2012年投入教育经费2500万元,预计2014年投入3600万元,设这两年投入教育经费的年平均增长百分率为x,则下列方程正确的是( )
A. 2500x2=3600 B. 2500(1+x)2=3600
C. 2500(1+x%)2=3600 D. 2500(1+x)+2500(1+x)2=3600
B 【解析】试题分析:2014年投入为2500(1+x),2015年投入为2500(1+x)(1+x),即2500(1+x)2=3600; 故选B.查看答案和解析>>
科目: 来源:人教版九年级上册数学 21.3实际问题与一元二次方程(1) 测试 题型:单选题
某镇2012年投入教育经费2000万元,为了发展教育事业,该镇每年教育经费的年增长率均为x,预计到2014年共投入9500万元,则下列方程正确的是( )
A. 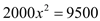
B. 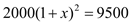
C. 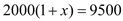
D. 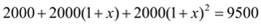
查看答案和解析>>
科目: 来源:人教版九年级上册数学 21.3实际问题与一元二次方程(1) 测试 题型:填空题
据调查,某市2012年的房价为4000元/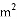 ,预计2014年将达到4840元/
,预计2014年将达到4840元/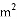 ,求这两年的年平均增长率,设年平均增长率为
,求这两年的年平均增长率,设年平均增长率为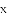
查看答案和解析>>
科目: 来源:人教版九年级上册数学 21.3实际问题与一元二次方程(1) 测试 题型:填空题
学校举行乒乓球比赛,有若干个队报名,比赛采取单循环制(每两个队要比赛一场),一共比了66场,则有___________个队参加了报名.
12 【解析】由题意得=66, , (x-12)(x+11)=0, 解得x1=12,x2=-11 所以有12个队参加了报名.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com