
科目: 来源:2017年甘肃省中考数学模拟试卷 题型:解答题
计算:(π﹣4)0+|3﹣tan60°|﹣(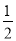 )﹣2+
)﹣2+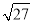 .
.
查看答案和解析>>
科目: 来源:2017年甘肃省中考数学模拟试卷 题型:解答题
解方程:2x2﹣4x+1=0.
x1=1+,x2=1﹣. 【解析】试题分析:先化二次项系数为1,然后把左边配成完全平方式,右边化为常数. 试题解析:由原方程,得 x2﹣2x=﹣, 等式的两边同时加上一次项系数一半的平方,得 x2﹣2x+1=, 配方,得 (x﹣1)2=, 直接开平方,得 x﹣1=± x1=1+,x2=1-.查看答案和解析>>
科目: 来源:2017年甘肃省中考数学模拟试卷 题型:解答题
如图,在每个小正方形的边长均为1的方格纸中,有线段AB,点A、B均在小正方形的顶点上.
(1)在方格纸中画出以AB为一边的等腰△ABC,点C在小正方形的顶点上,且△ABC的面积为6.
(2)在方格纸中画出△ABC的中线BD,并把线段BD绕点C逆时针旋转90°,画出旋转后的线段EF(B与E对应,D与F对应),连接BF,请直接写出BF的长.
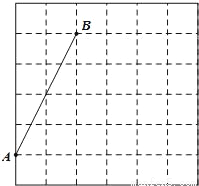
查看答案和解析>>
科目: 来源:2017年甘肃省中考数学模拟试卷 题型:解答题
“五一劳动节大酬宾!”,某商场设计的促销活动如下:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“50元”的字样.规定:在本商场同一日内,顾客每消费满300元,就可以在箱子里先后摸出两个球(第一次摸出后不放回).商场根据两小球所标金额的和返还相等价格的购物券,购物券可以在本商场消费.某顾客刚好消费300元.
(1)该顾客至多可得到 元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于50元的概率.
(1)70;(2). 【解析】试题分析:(1)由题意可得该顾客至多可得到购物券:50+20=70(元); (2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与该顾客所获得购物券的金额不低于50元的情况,再利用概率公式即可求得答案. 试题解析:(1)则该顾客至多可得到购物券:50+20=70(元); (2)画树状图得: ∵共有12种等可能的结果,该顾客所获得...查看答案和解析>>
科目: 来源:2017年甘肃省中考数学模拟试卷 题型:解答题
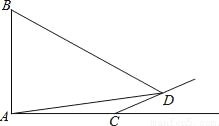
如图,旗杆AB的顶端B在夕阳的余辉下落在一个斜坡上的点D处,某校数学课外兴趣小组的同学正在测量旗杆的高度,在旗杆的底部A处测得点D的仰角为15°,AC=10米,又测得∠BDA=45°.已知斜坡CD的坡度为i=1: 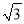 ,求旗杆AB的高度(
,求旗杆AB的高度(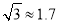 ,结果精确到个位).
,结果精确到个位).
查看答案和解析>>
科目: 来源:2017年甘肃省中考数学模拟试卷 题型:解答题
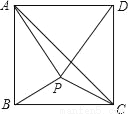
如图,在正方形ABCD内有一点P满足AP=AB,PB=PC,连接AC、PD.
求证:(1)△APB≌△DPC;(2)∠BAP=2∠PAC.
查看答案和解析>>
科目: 来源:2017年甘肃省中考数学模拟试卷 题型:解答题
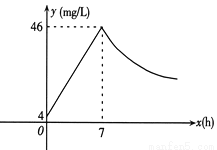
近年来,我国煤矿安全事故频频发生,其中危害最大的是瓦斯,其主要成分是CO.在一次矿难事件的调查中发现:从零时起,井内空气中CO的浓度达到4 mg/L,此后浓度呈直线型增加,在第7小时达到最高值46 mg/L,发生爆炸;爆炸后,空气中的CO浓度成反比例下降.如图11,根据题中相关信息回答下列问题:
(1)求爆炸前后空气中CO浓度y与时间x的函数关系式,并写出相应的自变量取值范围;
(2)当空气中的CO浓度达到34 mg/L时,井下3 km的矿工接到自动报警信号,这时他们至少要以多少km/h的速度撤离才能在爆炸前逃生?
(3)矿工只有在空气中的CO浓度降到4 mg/L及以下时,才能回到矿井开展生产自救,求矿工至少在爆炸后多少小时才能下井? (6+4+4=14分)
查看答案和解析>>
科目: 来源:2017年甘肃省中考数学模拟试卷 题型:解答题
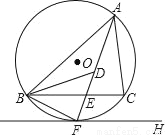
如图,⊙O是△ABC的外接圆,FH是⊙O的切线,切点为F,FH∥BC,连接AF交BC于E,∠ABC的平分线BD交AF于D,连接BF.
(1)证明:AF平分∠BAC;
(2)证明:BF=FD;
(3)若EF=4,DE=3,求AD的长.
查看答案和解析>>
科目: 来源:2017年甘肃省中考数学模拟试卷 题型:解答题
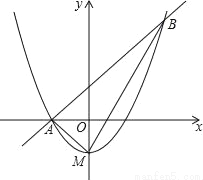
如图,顶点M在y轴上的抛物线与直线y=x+1相交于A、B两点,且点A在x轴上,点B的横坐标为2,连结AM、BM.
(1)求抛物线的函数关系式;
(2)判断△ABM的形状,并说明理由;
(3)把抛物线与直线y=x的交点称为抛物线的不动点.若将(1)中抛物线平移,使其顶点为(m,2m),当m满足什么条件时,平移后的抛物线总有不动点.
查看答案和解析>>
科目: 来源:江苏省句容市片区合作共同体2017-2018学年年八年级上学期第二次学情测试数学试卷 题型:单选题
在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com