
科目: 来源:2017年江苏省苏州市中考数学模拟试卷 题型:单选题
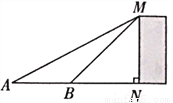
如图,为了测量某建筑物MN的高度,在平地上A处测得建筑物顶端M的仰角为30°,向N点方向前进16m到达B处,在B处测得建筑物顶端M的仰角为45°,则建筑物MN的高度等于( )
A. 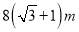 B.
B. 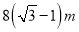 C.
C. 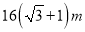 D.
D. 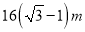
查看答案和解析>>
科目: 来源:2017年江苏省苏州市中考数学模拟试卷 题型:单选题
如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是 ( )
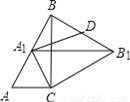
A. 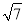 B.
B. 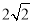 C. 3 D.
C. 3 D. 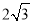
查看答案和解析>>
科目: 来源:2017年江苏省苏州市中考数学模拟试卷 题型:填空题
当a=2016时,分式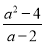 的值是_____.
的值是_____.
查看答案和解析>>
科目: 来源:2017年江苏省苏州市中考数学模拟试卷 题型:填空题
甲乙两人8次射击的成绩如图所示(单位:环).根据图中的信息判断,这8次射击中成绩比较稳定的是_____(填“甲”或“乙”).
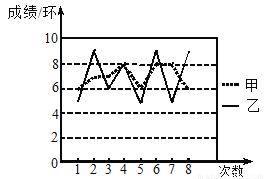
查看答案和解析>>
科目: 来源:2017年江苏省苏州市中考数学模拟试卷 题型:填空题
(2016江苏省苏州市)某学校计划购买一批课外读物,为了了解学生对课外读物的需求情况,学校进行了一次“我最喜爱的课外读物”的调查,设置了“文学”、“科普”、“艺术”和“其他”四个类别,规定每人必须并且只能选择其中一类,现从全体学生的调查表中随机抽取了部分学生的调查表进行统计,并把统计结果绘制了如图所示的两幅不完整的统计图,则在扇形统计图中,艺术类读物所在扇形的圆心角是________度.
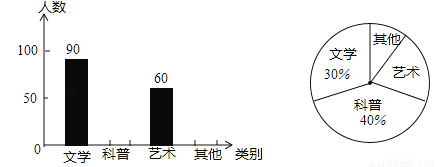
查看答案和解析>>
科目: 来源:2017年江苏省苏州市中考数学模拟试卷 题型:填空题
以方程组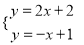 的解为坐标的点(x,y)在第_____象限.
的解为坐标的点(x,y)在第_____象限.
查看答案和解析>>
科目: 来源:2017年江苏省苏州市中考数学模拟试卷 题型:填空题
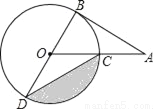
如图,AB为⊙O的切线,切点为B,连接AO,AO与⊙O交于点C,BD为⊙O的直径,连接CD,若∠A=30°,⊙O的半径为2,则图中阴影部分的面积为_____(结果保留π)
查看答案和解析>>
科目: 来源:2017年江苏省苏州市中考数学模拟试卷 题型:填空题
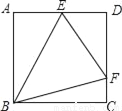
如图,正方形ABCD的边长为2,点E,F分别在边AD,CD上,若∠EBF=45°,则△EDF的周长等于_____.
查看答案和解析>>
科目: 来源:2017年江苏省苏州市中考数学模拟试卷 题型:填空题
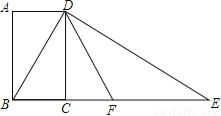
如图,四边形ABCD为矩形,过点D作对角线BD的垂线,交BC的延长线于点E,取BE的中点F,连接DF,DF=4.设AB=x,AD=y,则x2+(y﹣4)2的值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com