
科目: 来源:2017年山东省临沂市中考数学模拟试卷 题型:填空题
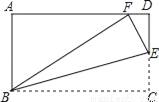
如图,在矩形ABCD中,AB=3,BC=5,在CD上任取一点E,连接BE,将△BCE沿BE折叠,使点C恰好落在AD边上的点F处,则CE的长为_____.
查看答案和解析>>
科目: 来源:2017年山东省临沂市中考数学模拟试卷 题型:填空题
如果一个数的平方等于﹣1,记为i2=﹣1,这个数i叫做虚数单位.那么和我们所学的实数对应起来就叫做复数,表示为a+bi(a,b为实数),a叫这个复数的实部,b叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.
如:(2+i)+(3﹣4i)=(2+3)+(1﹣4)i=5﹣3i,
(5+i)(3﹣4i)=5×3+5×(﹣4i)+i×3+i×(﹣4i)=15﹣20i+3i﹣4i2=19﹣17i
请根据以上内容的理解,利用以前学习的有关知识将(1+2i)(1﹣3i)化简结果为_____.
7﹣i 【解析】(1+2i)(1-3i)=1-3i+2i-6i² ∵i2=-1 ∴原式=1-i+6=7-i 故填:7-i查看答案和解析>>
科目: 来源:2017年山东省临沂市中考数学模拟试卷 题型:解答题
计算: 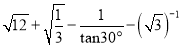 .
.
查看答案和解析>>
科目: 来源:2017年山东省临沂市中考数学模拟试卷 题型:解答题
初二年级教师对试卷讲评课中学生参与的深度与广度进行评价调查,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初二学生的参与情况,绘制成如图所示的频数分布直方图和扇形统计图(均不完整),请根据图中所给信息解答下列问题:
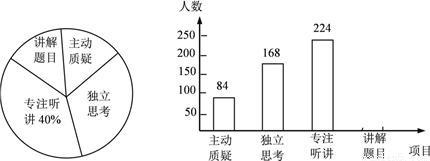
(1)在这次评价中,一共抽查了 名学生;
(2)在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为 度;
(3)请将频数分布直方图补充完整;
(4)如果全市有6000名初二学生,那么在试卷评讲课中,“独立思考”的初二学生约有多少人?
(1)560;(2)54 ;(3)见解析;(4)1800 【解析】试题分析:(1)、根据专注听讲的人数是224人,所占的比例是40%,即可求得抽查的总人数;(2)、利用360乘以对应的百分比即可求解;(3)、利用总人数减去其他各组的人数,即可求得讲解题目的人数,从而作出频数分布直方图;(4)、利用6000乘以对应的比例即可. 试题解析:(1)、调查的总人数是:224÷40%=560(人...查看答案和解析>>
科目: 来源:2017年山东省临沂市中考数学模拟试卷 题型:解答题
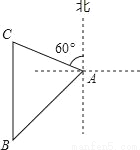
如图,海中一小岛有一个观测点A,某天上午观测到某渔船在观测点A的西南方向上的B处跟踪鱼群由南向北匀速航行.B处距离观测点30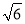 海里,若该渔船的速度为每小时30海里,问该渔船多长时间到达观测点A的北偏西60°方向上的C处?(计算结果用根号表示,不取近似值)
海里,若该渔船的速度为每小时30海里,问该渔船多长时间到达观测点A的北偏西60°方向上的C处?(计算结果用根号表示,不取近似值)
查看答案和解析>>
科目: 来源:2017年山东省临沂市中考数学模拟试卷 题型:解答题
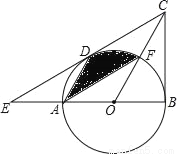
如图,在△BCE中,点A是边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF.
(1)求证:CB是⊙O的切线;
(2)若∠ECB=60°,AB=6,求图中阴影部分的面积.
查看答案和解析>>
科目: 来源:2017年山东省临沂市中考数学模拟试卷 题型:解答题
为改善生态环境,防止水土流失,某村计划在江汉堤坡种植白杨树,现甲、乙两家林场有相同的白杨树苗可供选择,其具体销售方案如下:
甲林场 | 乙林场 | ||
购树苗数量 | 销售单价 | 购树苗数量 | 销售单价 |
不超过1000棵时 | 4元/棵 | 不超过2000棵时 | 4元/棵 |
超过1000棵的部分 | 3.8元/棵 | 超过2000棵的部分 | 3.6元/棵 |
设购买白杨树苗x棵,到两家林场购买所需费用分别为y甲(元)、y乙(元).
(1)该村需要购买1500棵白杨树苗,若都在甲林场购买所需费用为 元,若都在乙林场购买所需费用为 元;
(2)分别求出y甲、y乙与x之间的函数关系式;
(3)如果你是该村的负责人,应该选择到哪家林场购买树苗合算,为什么?
(1)5900,6000;(2)y甲=,y乙=;(3)当0≤x≤1000或x=3000时,两家林场购买一样,当1000<x<3000时,到甲林场购买合算;x>3000时,到乙林场购买合算. 【解析】试题分析: (1)由单价×数量就可以得出购买树苗需要的费用; (2)根据分段函数的表示法,甲林场分或两种情况 .乙林场分或两种情况.由由单价×数量就可以得出购买树苗需要的费用表示出甲、乙与之间的...查看答案和解析>>
科目: 来源:2017年山东省临沂市中考数学模拟试卷 题型:解答题
如图①,△ABC是等腰直角三角形,∠BAC=90°,AB=AC,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时BD=CF,BD⊥CF成立.
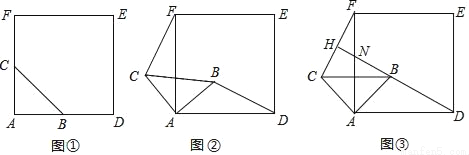
(1)当△ABC绕点A逆时针旋转α(0°<α<90°)时,如图②,BD=CF成立吗?若成立,请证明;若不成立,请说明理由;
(2)当△ABC绕点A逆时针旋转45°时,如图③,延长DB交CF于点H;
(ⅰ)求证:BD⊥CF;
(ⅱ)当AB=2,AD=3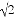 时,求线段DH的长.
时,求线段DH的长.
查看答案和解析>>
科目: 来源:2017年山东省临沂市中考数学模拟试卷 题型:解答题
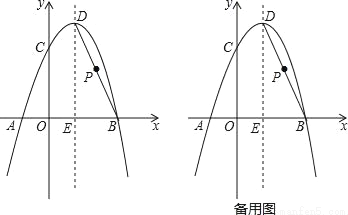
如图,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点,且与y轴交于点C,点D是抛物线的顶点,抛物线的对称轴DE交x轴于点E,连接BD.
(1)求经过A,B,C三点的抛物线的函数表达式;
(2)点P是线段BD上一点,当PE=PC时,求点P的坐标;
(3)在(2)的条件下,过点P作PF⊥x轴于点F,G为抛物线上一动点,M为x轴上一动点,N为直线PF上一动点,当以F、M、N、G为顶点的四边形是正方形时,请求出点M的坐标.
查看答案和解析>>
科目: 来源:浙江省宁波市2017-2018学年七年级上册期末模拟数学试卷 题型:单选题
下列运用等式性质进行的变形,其中不正确的是( )
A. 如果a=b,那么a+3=b+3 B. 如果a=b,那么a﹣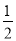 =b﹣
=b﹣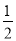
C. 如果a=b,那么ac=bc D. 如果a=b,那么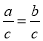
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com