
科目: 来源:黄金30题系列 九年级数学 大题易丢分 题型:解答题
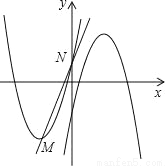
如图,在平面直角坐标系中,已知抛物线C1:y=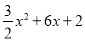 的顶点为M,与y轴相交于点N,先将抛物线C1沿x轴翻折,再向右平移p个单位长度后得到抛物线C2:直线l:y=kx+b经过M,N两点.
的顶点为M,与y轴相交于点N,先将抛物线C1沿x轴翻折,再向右平移p个单位长度后得到抛物线C2:直线l:y=kx+b经过M,N两点.
(1)结合图象,直接写出不等式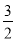 x2+6x+2<kx+b的解集;
x2+6x+2<kx+b的解集;
(2)若抛物线C2的顶点与点M关于原点对称,求p的值及抛物线C2的解析式;
(3)若直线l沿y轴向下平移q个单位长度后,与(2)中的抛物线C2存在公共点,
求3﹣4q的最大值.
【答案】(1)﹣2<x<0(2)y=﹣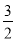 x2+6x﹣2(3)当q=
x2+6x﹣2(3)当q= 时,3﹣4q取最大值,最大值为﹣7
时,3﹣4q取最大值,最大值为﹣7
【解析】试题分析:(1)、首先根据二次函数的解析式分别求出点M和点N的坐标,然后根据图像得出不等式的取值范围;(2)、根据翻折得出抛物线的顶点坐标和开口方向以及大小,从而得出抛物线的函数解析式;(3)、首先将点M和点N的坐标代入一次函数解析式得出一次函数的解析式,然后设平移后的解析式为y=3x+2-q,然后根据与抛物线有交点得出方程有实数根,从而得出最大值.
试题解析:(1)令y=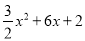 中x=0,则y=2,
中x=0,则y=2,
∴N(0,2); ∵y=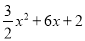 =
=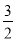 (x+2)2﹣4, ∴M(﹣2,﹣4).
(x+2)2﹣4, ∴M(﹣2,﹣4).
观察函数图象,发现:当﹣2<x<0时,抛物线C1在直线l的下方,
∴不等式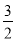 x2+6x+2<kx+b的解集为﹣2<x<0.
x2+6x+2<kx+b的解集为﹣2<x<0.
(2)∵抛物线C1:y=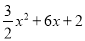 的顶点为M(﹣2,﹣4),
的顶点为M(﹣2,﹣4),
沿x轴翻折后的对称点坐标为(﹣2,4). ∵抛物线C2的顶点与点M关于原点对称,
∴抛物线C2的顶点坐标为(2,4), ∴p=2﹣(﹣2)=4.
∵抛物线C2与C1开口大小相同,开口方向相反,
∴抛物线C2的解析式为y=﹣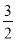 (x﹣2)2+4=﹣
(x﹣2)2+4=﹣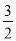 x2+6x﹣2.
x2+6x﹣2.
(3)将M(﹣2,﹣4)、N(0,2)代入y=kx+b中,得: 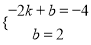 ,解得:
,解得: 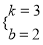 ,
,
∴直线l的解析式为y=3x+2.
∵若直线l沿y轴向下平移q个单位长度后与抛物线C2存在公共点,
∴方程﹣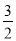 x2+6x﹣2=3x+2﹣q有实数根,即3x2﹣6x+8﹣2q有实数根,
x2+6x﹣2=3x+2﹣q有实数根,即3x2﹣6x+8﹣2q有实数根,
∴△=(﹣6)2﹣4×3×(8﹣2q)≥0,解得:q≥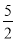 . ∵﹣4<0,
. ∵﹣4<0,
∴当q=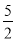 时,3﹣4q取最大值,最大值为﹣7.
时,3﹣4q取最大值,最大值为﹣7.
点睛:本题主要考查的就是二次函数的图形与性质、一次函数的性质、二次函数与一次函数的大小比较的方法以及函数与方程之间的关系,属于中上难度的题目.在解答函数大小比较的题目时,我们首先根据方程的思想得出两个函数的交点坐标,然后过交点作x轴的垂线,然后根据函数所处的位置进行比较大小得出答案;函数关于x轴对称,则顶点坐标的纵坐标变为相反数,开口方向发生改变,开口大小不改变;在求直线与抛物线是否有交点时,则联立成方程,然后根据一元二次方程根的判别式来进行判定.
【题型】解答题
【结束】
17
某商家经销一种绿茶,用于装修门面已投资3000元.已知绿茶每千克成本50元,经研究发现销量y(kg)随销售单价x(元/ kg)的变化而变化,具体变化规律如下表所示:

设该绿茶的月销售利润为w(元)(销售利润=单价×销售量-成本)
(1)请根据上表,求出y与x之间的函数关系式(不必写出自变量x的取值范围);
(2)求w与x之间的函数关系式(不必写出自变量x的取值范围),并求出x为何值时,w的值最大?
(3)若在第一个月里,按使w获得最大值的销售单价进行销售后,在第二个月里受物价部门干预,销售单价不得高于80元,要想在全部收回装修投资的基础上使第二个月的利润至少达到1700元,那么第二个月时里应该确定销售单价在什么范围内?
(1); (2),当时, ; (3)当销售单价为元时,在全部收回投资的基础上使第二个月的利润不低于1700元. 【解析】【试题分析】(1)根据表格的数据.易得销售单价每升高5元,销售量下降10Kg,即w是x的一次函数,故设设,将(70,100),(75,90)代入上式得: 解得: ,则; (2)销售利润=单位质量的利润乘以销售量,即 ,化为顶点式得, ,当时, ...查看答案和解析>>
科目: 来源:黄金30题系列 九年级数学 大题易丢分 题型:解答题
某商家经销一种绿茶,用于装修门面已投资3000元.已知绿茶每千克成本50元,经研究发现销量y(kg)随销售单价x(元/ kg)的变化而变化,具体变化规律如下表所示:

设该绿茶的月销售利润为w(元)(销售利润=单价×销售量-成本)
(1)请根据上表,求出y与x之间的函数关系式(不必写出自变量x的取值范围);
(2)求w与x之间的函数关系式(不必写出自变量x的取值范围),并求出x为何值时,w的值最大?
(3)若在第一个月里,按使w获得最大值的销售单价进行销售后,在第二个月里受物价部门干预,销售单价不得高于80元,要想在全部收回装修投资的基础上使第二个月的利润至少达到1700元,那么第二个月时里应该确定销售单价在什么范围内?
【答案】(1)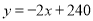 ;
;
(2)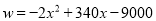 ,当
,当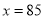 时,
时, 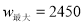 ;
;
(3)当销售单价为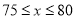 元时,在全部收回投资的基础上使第二个月的利润不低于1700元.
元时,在全部收回投资的基础上使第二个月的利润不低于1700元.
【解析】【试题分析】(1)根据表格的数据.易得销售单价每升高5元,销售量下降10Kg,即w是x的一次函数,故设设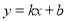 ,将(70,100),(75,90)代入上式得:
,将(70,100),(75,90)代入上式得:
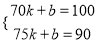 解得:
解得: 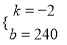 ,则
,则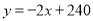 ;
;
(2)销售利润=单位质量的利润乘以销售量,即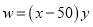
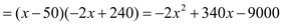 ,化为顶点式得,
,化为顶点式得, 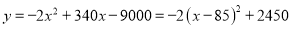 ,当
,当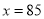 时,
时, 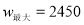
(3)由(2)知,第1个月还有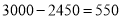 元的投资成本没有收回.则要想在全部收投资的基础上使第二个月的利润达到1700元, 即
元的投资成本没有收回.则要想在全部收投资的基础上使第二个月的利润达到1700元, 即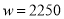 才可以,可得方程
才可以,可得方程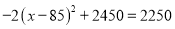 ,解得:
,解得: 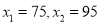 根据题意
根据题意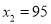 不合题意,应舍去.当
不合题意,应舍去.当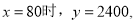 ,因为-2<0,则抛物线开口向下,当
,因为-2<0,则抛物线开口向下,当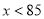 时,
时, 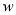 随
随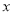 的增大而增大,当
的增大而增大,当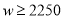 ,且销售单价不高于80时,
,且销售单价不高于80时, 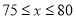
【试题解析】
(1)设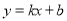 ,将(70,100),(75,90)代入上式得:
,将(70,100),(75,90)代入上式得:
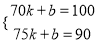 解得:
解得: 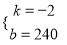 ,则
,则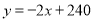 ,
,
将表中其它对应值代入上式均成立,所以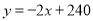
(2)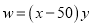
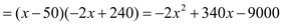
因此, 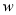 与
与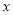 的关系式为
的关系式为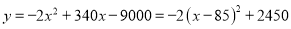
当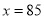 时,
时, 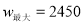
(3)由(2)知,第1个月还有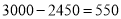 元的投资成本没有收回.
元的投资成本没有收回.
则要想在全部收投资的基础上使第二个月的利润达到1700元, 即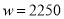 才可以,
才可以,
可得方程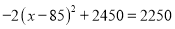 ,解得:
,解得: 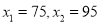
根据题意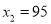 不合题意,应舍去.当
不合题意,应舍去.当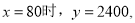 ,
,
∵-2<0,∴,当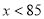 时,
时, 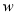 随
随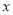 的增大而增大,
的增大而增大,
当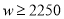 ,且销售单价不高于80时,
,且销售单价不高于80时, 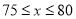
答:当销售单价为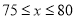 元时,在全部收回投资的基础上使第二个月的利润不低于1700元
元时,在全部收回投资的基础上使第二个月的利润不低于1700元
【题型】解答题
【结束】
18
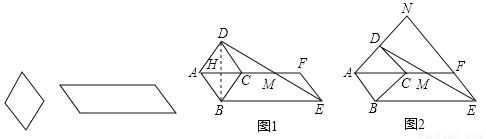
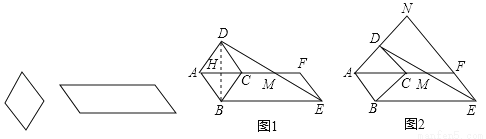
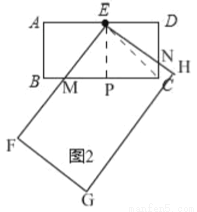
如图,分别是可活动的菱形和平行四边形学具,已知平行四边形较短的边与菱形的边长相等.
(1)在一次数学活动中,某小组学生将菱形的一边与平行四边形较短边重合,摆拼成如图1所示的图形,AF经过点C,连接DE交AF于点M,观察发现:点M是DE的中点.
下面是两位学生有代表性的证明思路:
思路1:不需作辅助线,直接证三角形全等;
思路2:不证三角形全等,连接BD交AF于点H.…
请参考上面的思路,证明点M是DE的中点(只需用一种方法证明);
(2)如图2,在(1)的前提下,当∠ABE=135°时,延长AD、EF交于点N,求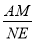 的值;
的值;
(3)在(2)的条件下,若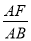 =k(k为大于
=k(k为大于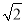 的常数),直接用含k的代数式表示
的常数),直接用含k的代数式表示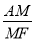 的值.
的值.
查看答案和解析>>
科目: 来源:黄金30题系列 九年级数学 大题易丢分 题型:解答题
如图,分别是可活动的菱形和平行四边形学具,已知平行四边形较短的边与菱形的边长相等.
(1)在一次数学活动中,某小组学生将菱形的一边与平行四边形较短边重合,摆拼成如图1所示的图形,AF经过点C,连接DE交AF于点M,观察发现:点M是DE的中点.
下面是两位学生有代表性的证明思路:
思路1:不需作辅助线,直接证三角形全等;
思路2:不证三角形全等,连接BD交AF于点H.…
请参考上面的思路,证明点M是DE的中点(只需用一种方法证明);
(2)如图2,在(1)的前提下,当∠ABE=135°时,延长AD、EF交于点N,求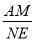 的值;
的值;
(3)在(2)的条件下,若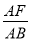 =k(k为大于
=k(k为大于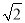 的常数),直接用含k的代数式表示
的常数),直接用含k的代数式表示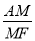 的值.
的值.
【答案】(1)证明见解析;(2)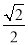 ;(3)
;(3)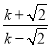 .
.
【解析】试题分析:(1)证法一,利用菱形性质得AB=CD,AB∥CD,利用平行四边形的性质得AB=EF,AB∥EF,则CD=EF,CD∥EF,再根据平行线的性质得∠CDM=∠FEM,则可根据“AAS”判断△CDM≌△FEM,所以DM=EM;
证法二,利用菱形性质得DH=BH,利用平行四边形的性质得AF∥BE,再根据平行线分线段成比例定理得到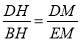 =1,所以DM=EM;
=1,所以DM=EM;
(2)由△CDM≌△FEM得到CM=FM,设AD=a,CM=b,则FM=b,EF=AB=a,再证明四边形ABCD为正方形得到AC=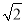 a,接着证明△ANF为等腰直角三角形得到NF=a+
a,接着证明△ANF为等腰直角三角形得到NF=a+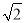 b,则NE=NF+EF=2a+
b,则NE=NF+EF=2a+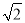 b,然后计算
b,然后计算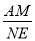 的值;
的值;
(3)由于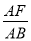 =
=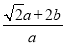 =
=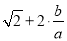 =k,则
=k,则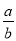 =
=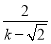 ,然后表示出
,然后表示出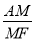 =
=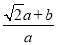 =
=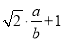 ,再把
,再把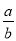 =
=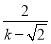 代入计算即可.
代入计算即可.
试题解析:【解析】
(1)如图1,证法一:∵四边形ABCD为菱形,∴AB=CD,AB∥CD,∵四边形ABEF为平行四边形,∴AB=EF,AB∥EF,∴CD=EF,CD∥EF,∴∠CDM=∠FEM,在△CDM和△FEM中,∵∠CMD=∠FME,∠CDM=∠FEM,CD=EF,∴△CDM≌△FEM,∴DM=EM,即点M是DE的中点;
证法二:∵四边形ABCD为菱形,∴DH=BH,∵四边形ABEF为平行四边形,∴AF∥BE,∵HM∥BE,∴ 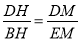 =1,∴DM=EM,即点M是DE的中点;
=1,∴DM=EM,即点M是DE的中点;
(2)∵△CDM≌△FEM,∴CM=FM,设AD=a,CM=b,∵∠ABE=135°,∴∠BAF=45°,∵四边形ABCD为菱形,∴∠NAF=45°,∴四边形ABCD为正方形,∴AC=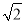 AD=
AD=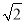 a,∵AB∥EF,∴∠AFN=∠BAF=45°,∴△ANF为等腰直角三角形,∴NF=
a,∵AB∥EF,∴∠AFN=∠BAF=45°,∴△ANF为等腰直角三角形,∴NF=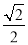 AF=
AF=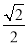 (
(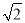 a+b+b)=a+
a+b+b)=a+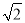 b,∴NE=NF+EF=a+
b,∴NE=NF+EF=a+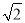 b+a=2a+
b+a=2a+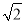 b,∴
b,∴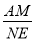 =
=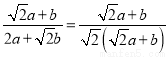 =
=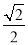 ;
;
(3)∵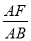 =
=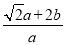 =
=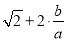 =k,∴
=k,∴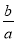 =
=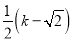 ,∴
,∴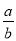 =
=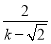 ,∴
,∴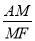 =
=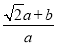 =
=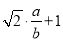 =
=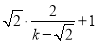 =
=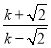 .
.
点睛:本题考查了相似形的综合题:熟练掌握平行线分线段成比例定理、平行四边形和菱形的性质;灵活利用全等三角形的知识解决线段相等的问题;会利用代数法表示线段之间的关系.
【题型】解答题
【结束】
19
问题背景
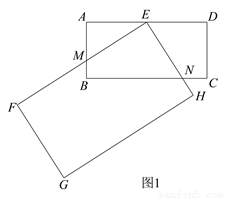
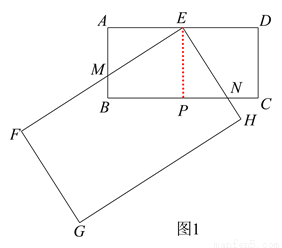
在数学活动课上,张老师要求同学们拿两张大小不同的矩形纸片进行旋转变换探究活动.如图 1,在矩形纸片ABCD 和矩形纸片EFGH中,AB=1,AD=2,且FE>AD,FG>AB,点E 是 AD 的中点,矩形纸片 EFGH 以点E 为旋转中心进行逆时针旋转,在旋转过程中会产生怎样的数量关系,提出恰当的数学问题并加以解决.
解决问题
下面是三个学习小组提出的数学问题,请你解决这些问题.
(1)“奋进”小组提出的问题是:如图 1,当 EF 与 AB 相交于点 M,EH 与 BC 相交于点 N 时,求证:EM=EN.
(2)“雄鹰”小组提出的问题是:在(1)的条件下,当 AM=CN 时,AM 与 BM 有怎样的数量关系,请说明理由.
(3)“创新”小组提出的问题是:若矩形 EFGH 继续以点 E 为旋转中心进行逆时针旋转,当 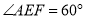 时,请你在图 2 中画出旋转后的示意图,并求出此时 EF 将边 BC 分成的两条线段的长度.
时,请你在图 2 中画出旋转后的示意图,并求出此时 EF 将边 BC 分成的两条线段的长度.

查看答案和解析>>
科目: 来源:黄金30题系列 九年级数学 大题易丢分 题型:解答题
问题背景
在数学活动课上,张老师要求同学们拿两张大小不同的矩形纸片进行旋转变换探究活动.如图 1,在矩形纸片ABCD 和矩形纸片EFGH中,AB=1,AD=2,且FE>AD,FG>AB,点E 是 AD 的中点,矩形纸片 EFGH 以点E 为旋转中心进行逆时针旋转,在旋转过程中会产生怎样的数量关系,提出恰当的数学问题并加以解决.
解决问题
下面是三个学习小组提出的数学问题,请你解决这些问题.
(1)“奋进”小组提出的问题是:如图 1,当 EF 与 AB 相交于点 M,EH 与 BC 相交于点 N 时,求证:EM=EN.
(2)“雄鹰”小组提出的问题是:在(1)的条件下,当 AM=CN 时,AM 与 BM 有怎样的数量关系,请说明理由.
(3)“创新”小组提出的问题是:若矩形 EFGH 继续以点 E 为旋转中心进行逆时针旋转,当 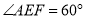 时,请你在图 2 中画出旋转后的示意图,并求出此时 EF 将边 BC 分成的两条线段的长度.
时,请你在图 2 中画出旋转后的示意图,并求出此时 EF 将边 BC 分成的两条线段的长度.
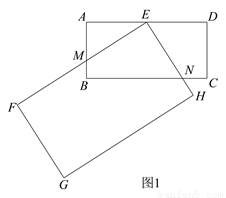

【答案】(1)证明见解析;(2)AM=BN;(3)EF 将边 BC 分成的两条线段的长度为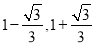 .
.
【解析】试题分析:(1)过点 E 作 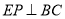 ,垂足为点P,根据已知条件证出PE=AE,再证得∠PEN=∠AEM,进而得到△PEN≌△AEM,即可证得结论;(2)易证PN=CN=
,垂足为点P,根据已知条件证出PE=AE,再证得∠PEN=∠AEM,进而得到△PEN≌△AEM,即可证得结论;(2)易证PN=CN= 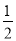 PC,进而求出PN=CN=
PC,进而求出PN=CN=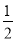 ,再判断出AM=PN=
,再判断出AM=PN=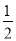 ,即可得出BM=
,即可得出BM=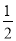 ,从而证得结论;(3)在Rt△PEM中,求出PM的长,再用线段的和差即可得出结论.
,从而证得结论;(3)在Rt△PEM中,求出PM的长,再用线段的和差即可得出结论.
试题解析:
(1) 如图1,过点 E 作 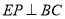 ,垂足为点 P,
,垂足为点 P,
则四边形 ABPE 是矩形,∴PE=AB=1, 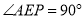 ,
,
∵ 点 E 是 AD 的中点,∴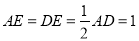 ,∴PE=AE,
,∴PE=AE,
∵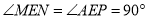 ,∴
,∴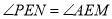 ,
,
∵PE=AE, 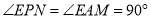 ,∴
,∴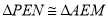 ,∴EM=EN.
,∴EM=EN.
(2) 由(1)知, 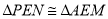 ,∴AM=PN,
,∴AM=PN,
∵AM=CN,∴PN=CN=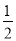 PC,
PC,
∵ 四边形 EPCD 是矩形,∴PC=DE=1,PN=CN=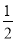 ,
,
∴AM=PN=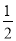 ,BM=AB-AM=
,BM=AB-AM=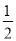 ,∴AM=BN.
,∴AM=BN.
(3)如图2,当∠AEF=60°时,
设EF与BC交于M,EH与CD交于N,过点E作EP⊥BC于P,连接EC,
由(1)知,CP=EP=1,AD∥BC,
∴∠EMP=∠AEF=60°,
在Rt△PEM中,PM=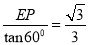 ,
,
∴BM=BP﹣PM=1﹣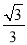 ,CM=PC+PM=1+
,CM=PC+PM=1+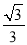 ,
,
∴EF将边BC分成的两条线段的长度为1﹣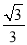 ,1+
,1+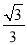 .
.
【题型】解答题
【结束】
20
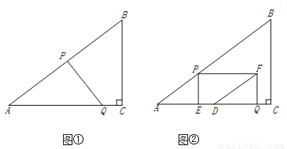
如图①,在Rt△ABC中,∠C=90°,AB=10,BC=6.点P从点A出发,沿折现AB—BC向终点C运动,在AB上以每秒5个单位长度的速度运动,在BC上以每秒3个单位长度的速度运动.点Q从点C出发,沿CA方向以每秒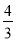 个单位长度的速度运动.点P、Q两点同时出发,当点P停止时,点Q也随之停止.设点P运动的时间为t秒.
个单位长度的速度运动.点P、Q两点同时出发,当点P停止时,点Q也随之停止.设点P运动的时间为t秒.
(1)求线段AQ的长.(用含t的代数式表示)
(2)当PQ与△ABC的一边平行时,求t的值
(3)如图②,过点P作PE⊥AC于点E,以PE、QE为邻边作矩形PEQF,点D为AC的中点,连结DF.直接写出DF将矩形PEQF分成两部分的面积比为1:2时t的值.
查看答案和解析>>
科目: 来源:2017年贵州省中考数学二模试卷 题型:单选题
﹣5的倒数的相反数是( )
A. 5 B. 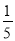 C. ﹣5 D. ﹣
C. ﹣5 D. ﹣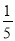
查看答案和解析>>
科目: 来源:2017年贵州省中考数学二模试卷 题型:单选题
下列运算正确的是
A.x•x2=x2 B.(xy)2=xy2 C.(x2)3=x6 D.x2+x2=x4
C 【解析】 试题分析:根据同底数幂的乘法,幂的乘方与积的乘方,合并同类项运算法则逐一计算作出判断: A、x•x2=x1+2=x3≠x2,故本选项错误; B、(xy)2=x2y2≠xy2,故本选项错误; C、(x2)3=x2×3=x6,故本选项正确; D、x2+x2=2x2=x4,故本选项错误。 故选C。查看答案和解析>>
科目: 来源:2017年贵州省中考数学二模试卷 题型:单选题
一组数据2、5、4、3、5、4、5的中位数和众数分别是( ).
A.3.5,5 B.4,4 C.4,5 D.4.5,4
C. 【解析】 试题分析:根据众数和中位数的概念求解.这组数据按照从小到大的顺序排列为:2,3,4,4,5,5,5,则众数为5,中位数为4. 故选:C.查看答案和解析>>
科目: 来源:2017年贵州省中考数学二模试卷 题型:单选题
从1~9这九个自然数中任取一个,是2的倍数的概率是 ( )
A.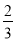 B.
B.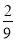 C.
C.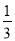 D.
D.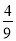
查看答案和解析>>
科目: 来源:2017年贵州省中考数学二模试卷 题型:单选题
如图,在△ABC中,点D、E分AB、AC边上,DE∥BC,若AD:AB=3:4,AE=6,则AC等于( )
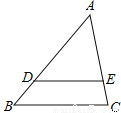
A.3 B.4 C.6 D.8
D 【解析】 首先由DE∥BC可以得到AD:AB=AE:AC,而AD:AB=3:4,AE=6,由此即可求出AC. 【解析】 ∵DE∥BC, ∴△ADE∽△ABC, ∴AD:AB=AE:AC, 而AD:AB=3:4,AE=6, ∴3:4=6:AC, ∴AC=8. 故选D.查看答案和解析>>
科目: 来源:2017年贵州省中考数学二模试卷 题型:单选题
如图是由我市某中学楼层间的两个台阶组成的几何体,已知两个台阶的高度和宽度是相同的,据此可判断此几何体的三视图是( ).
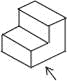
A. 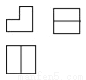
B. 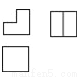
C. 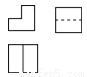
D. 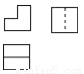
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com