相关习题
0 319765 319773 319779 319783 319789 319791 319795 319801 319803 319809 319815 319819 319821 319825 319831 319833 319839 319843 319845 319849 319851 319855 319857 319859 319860 319861 319863 319864 319865 319867 319869 319873 319875 319879 319881 319885 319891 319893 319899 319903 319905 319909 319915 319921 319923 319929 319933 319935 319941 319945 319951 319959 366461
科目:
来源:山西省2017-2018学年八年级上期末模拟数学试卷
题型:填空题
如图,已知AB=DE,BC=EF,若要使△ABC≌△DEF,那么还要需要一个条件,这个条件可以是: ________
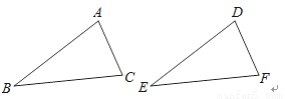
AC=DF
【解析】如图,已知AB=DE,BC=EF,添加条件AC=DF,利用SSS即可证明△ABC≌△DEF;添加条件∠B=∠E,利用SAS即可证明△ABC≌△DEF.答案不唯一,写出一个即可.
查看答案和解析>>
科目:
来源:山西省2017-2018学年八年级上期末模拟数学试卷
题型:填空题
如图,若?ABCD的周长为36cm,过点D分别作AB,BC边上的高DE,DF,且DE=4cm,DF=5cm,?ABCD的面积为 cm2.
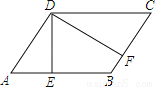
40
【解析】
试题分析:由?ABCD的周长为36cm,可得AB+BC=18cm①,又由过点D分别作AB,BC边上的高DE,DF,且DE=4cm,DF=5cm,由等积法,可得4AB=5BC②,继而求得答案.
【解析】
∵?ABCD的周长为36cm,
∴AB+BC=18cm①,
∵过点D分别作AB,BC边上的高DE,DF,且DE=4cm,DF=5cm,
∴4AB...
查看答案和解析>>
科目:
来源:山西省2017-2018学年八年级上期末模拟数学试卷
题型:填空题
用反证法证明AB≠AC时,首先假设________成立.
AB=AC
【解析】反证法的步骤是:(1)假设结论不成立;(2)从假设出发推出矛盾;(3)假设不成立,则结论成立. 由此可得用反证法证明AB≠AC时,首先假设AB=AC成立.
查看答案和解析>>
科目:
来源:山西省2017-2018学年八年级上期末模拟数学试卷
题型:填空题
在实数范围内因式分【解析】
x3﹣2x2y+xy2=________.
x(x﹣y)2
【解析】提公因式x后再利用完全平方公式分解即可,即原式= .
查看答案和解析>>
科目:
来源:山西省2017-2018学年八年级上期末模拟数学试卷
题型:填空题
如图,已知AB=BC,要使△ABD≌△CBD,还需添加一个条件,你添加的条件是 ________ (只需写一个,不添加辅助线)
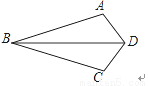
∠ABD=∠CBD或AD=CD
【解析】试题分析:由已知AB=BC,及公共边BD=BD,可知要使△ABD≌△CBD,已经具备了两个S了,然后根据全等三角形的判定定理,应该有两种判定方法①SAS,②SSS.所以可添∠ABD=∠CBD或AD=CD.
【解析】
答案不唯一.
①∠ABD=∠CBD.
在△ABD和△CBD中,
∵,
∴△ABD≌△CBD(SAS);
...
查看答案和解析>>
科目:
来源:山西省2017-2018学年八年级上期末模拟数学试卷
题型:填空题
如图,已知△ABC中,AB=BD=DC,∠ABC=105°,求∠A,∠C度数.
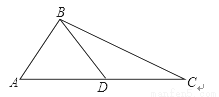
∠A=50°,∠C=25°.
【解析】试题分析:由于AB=BD=DC,所以△ABD和△BDC都是等腰三角形,可设∠C=∠CDB=x,则∠BDA=∠A=2x,根据等腰三角形的性质和三角形内角和定理的推论,可以求出∠A,∠C度数.
试题解析:
∵AB=BD,
∴∠BDA=∠A,
∵BD=DC,
∴∠C=∠CBD,
设∠C=∠CBD=x,
则∠BDA=∠A...
查看答案和解析>>
科目:
来源:山西省2017-2018学年八年级上期末模拟数学试卷
题型:解答题
如图所示,点D在AC上,点E在AB上,且AB=AC,BC=BD,AD=DE=EB,求∠A的度数.
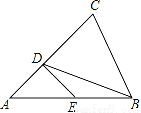
45°.
【解析】试题分析:由线段相等,可得对应角相等,通过转化,将∠A、∠ABC都与∠DBE建立联系,从而即可求解∠A的值.
试题解析:∵AB=AC,
∴∠ABC=∠C,又BC=BD,
∴∠BDC=∠C,
∵∠A+∠C+∠ABC=180°,∠DBC+∠C+∠BDC=180°,
∴∠DBC=∠A,
∵AD=DE=EB,
∴∠A=∠AED,∠EDB=∠...
查看答案和解析>>
科目:
来源:山西省2017-2018学年八年级上期末模拟数学试卷
题型:解答题
如图,在?ABCD中,M,N在对角线AC上,且AM=CN,求证:BM∥DN.
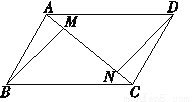
证明见解析.
【解析】试题分析:连接BD、MD、BN,根据平行四边形的性质证明OM=ON,然后再证明四边形BNDM是平行四边形,从而可得BM∥DN.
试题解析:连接BD、MD、BN,
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵AM=CN,
∴OA-AM=OC-CN,
即OM=ON,
∴四边形BNDM是平行四边形.
∴BM∥D...
查看答案和解析>>
科目:
来源:山西省2017-2018学年八年级上期末模拟数学试卷
题型:解答题
如图,AB=AC,BD=DC,DF⊥AB,DE⊥AC,垂足分别是F,E.求证:DE=DF.
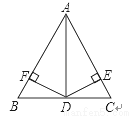
证明见解析.
【解析】试题分析:要证DE=DF,只需证△BDF≌△CDE,已知AB=AC,可得∠B=∠C,又已知BD=DC,∠BFD=∠CED=90°,则两三角形全等可证.
试题解析:∵AB=AC,∴∠B=∠C,
∵DE⊥AB,DF⊥AC,∴∠BFD=∠CED=90°,
∵BD=DC,∴△BDF≌△CDE,
∴DE=DF.
查看答案和解析>>
科目:
来源:山西省2017-2018学年八年级上期末模拟数学试卷
题型:解答题
如图,铁路上A,B两点相距25 km,C,D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=15 km,CB=10 km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少千米处?
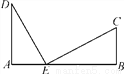
E站应建在离A站10千米处.
【解析】试题分析:根据C、D两村到E站的距离相等,可得DE=CE,在Rt△AED和Rt△EBC中,根据勾股定理可得AE2+AD2=BE2+BC2,设AE=x,则BE=25﹣x,列出方程,解方程求得x的值,即可得收购站E离A点的距离.
试题解析:
∵使得C,D两村到E站的距离相等.
∴DE=CE,
∵DA⊥AB于A,CB⊥AB于B,
...
查看答案和解析>>








