如图，是由边长为1的小正方形构成的网格，各个小正方形的顶点称之为格点，点A、C、E、F均在格点上，根据不同要求，选择格点，画出符合条件的图形：

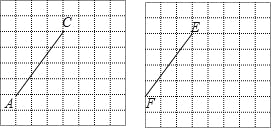
（1）在图1中，画一个以AC为一边的△ABC，使∠ABC=45°（画出一个即可）；

（2）在图2中，画一个以EF为一边的△DEF，使tan∠EDF=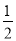，并直接写出线段DF的长．

（1）画图见解析．（2）DF==4； 【解析】 试题分析：（1）利用网格特点，AB在水平格线上，BC为4×4的正方形的对角线； （2）由于tan∠EDF=，则在含∠D的直角三角形中，满足对边与邻边之比为1：2即可． 试题解析：（1）如图1，△ABC为所作； （2）如图2，△DEF为所作，DF==4．

为便于管理与场地安排，松北某中学校以小明所在班级为例，对学生参加各个体育项目进行了调查统计．并把调查的结果绘制了如图所示的不完全统计图，请你根据下列信息回答问题：

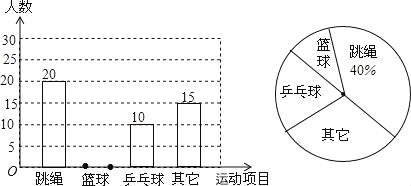
（1）在这次调查中，小明所在的班级参加篮球项目的同学有多少人？并补全条形统计图．

（2）如果学校有800名学生，请估计全校学生中有多少人参加篮球项目．

（1）5人，画图见解析．（2）80人； 【解析】 试题分析：（1）根据跳绳人数除以跳绳人数所占的百分比，可得抽查总人数，根据有理数的减法，可得参加篮球项目的人数，根据参加篮球项目的人数，可得答案； （2）根据全校学生人数乘以参加篮球项目所占的百分比，可得答案． 试题解析：（1）抽查总人数是：20÷40%=50（人）， 参加篮球项目的人数是：50﹣20﹣10﹣15=5（...

如图，△ABC中，∠ACB=90°，∠A=30°，CD为△ABC的中线，作CO⊥AB于O，点E在CO延长线上，DE=AD，连接BE、DE．

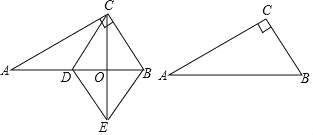
（1）求证：四边形BCDE为菱形；

（2）把△ABC分割成三个全等的三角形，需要两条分割线段，若AC=6，求两条分割线段长度的和．

（1）求证见解析．（2）6； 【解析】 试题分析：（1）容易证三角形BCD为等边三角形，又DE=AD=BD，再证三角形DBE为等边三角形四边相等的四边形BCDE为菱形． （2）画出图形，证出BM+MN=AM+MC=AC=6即可． 试题解析：（1）∵∠ACB=90°，∠A=30°，CD为△ABC的中线， ∴BC=AB，CD==AB=AD， ∴∠ACD=∠A=30°...

某商厦进货员预测一种应季衬衫能畅销市场，就用0.8万元购进这种衬衫，面市后果然供不应求．于是，商厦又用1.76万元购进了第二批这种衬衫，所购数量是第一批购进数量的2倍，但单价贵了4元，商厦销售这种衬衫时每件预定售价都是58元．

（1）求这种衬衫原进价为每件多少元？

（2）经过一段时间销售，根据市场饱和情况，商厦经理决定对剩余的100件衬衫进行打折销售，以提高回款速度，要使这两批衬衫的总利润不少于6300元，最多可以打几折？

（1）40．（2）5折； 【解析】 试题分析：（1）设这种衬衫原进价为每件x元．根据“用1.76万元购进了第二批这种衬衫，所购数量是第一批购进数量的2倍，但单价贵了4元”列出方程并解答，注意需要验根； （2）设打m折，根据题意列出不等式即可． 试题解析：（1）设这种衬衫原进价为每件x元 =， 解得：x=40． 经检验：x=40是原分式方程的解， 答：...

已知，AB、AC是圆O的两条弦，AB=AC，过圆心O作OH⊥AC于点H．

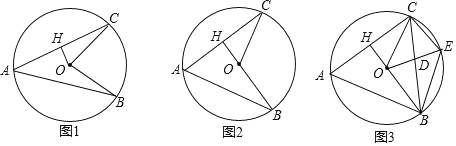
（1）如图1，求证：∠B=∠C；

（2）如图2，当H、O、B三点在一条直线上时，求∠BAC的度数；

（3）如图3，在（2）的条件下，点E为劣弧BC上一点，CE=6，CH=7，连接BC、OE交于点D，求BE的长和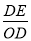的值．

（1）证明见解析．（2）∠BAC=60°； （3）BM=5，=. 【解析】 试题分析：（1）如图1中，连接OA．欲证明∠B=∠C，只要证明△AOC≌△AOB即可． （2）由OH⊥AC，推出AH=CH，由H、O、B在一条直线上，推出BH垂直平分AC，推出AB=BC，由AB=AC，推出AB=AC=BC，推出△ABC为等边三角形，即可解决问题． （3）过点B作BM⊥CE延长...

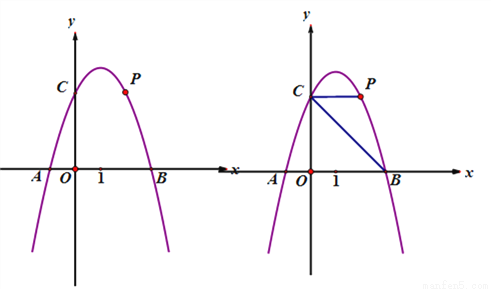
如图，抛物线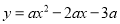交X轴于点A、B（A左B右），交Y轴于点C，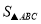

=6，点P为第一象限内抛物线上的一点.

（1）求抛物线的解析式；

（2）若∠PCB=45°，求点P的坐标；

（3）点Q为第四象限内抛物线上一点，点Q的横坐标比点P的横坐标大1，连接PC、

AQ，当PC=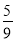AQ时，求点P的坐标以及ΔPCQ的面积.

（1）y=?x²+2x+3；（2）P(2,3)；（3）P(,)， . 【解析】试题分析：（1）根据抛物线的解析式求得点A、B、C的坐标，根据， =6即可求得a值，从而求得抛物线的解析式；（2）根据点B、C的坐标判定△OBC是等腰直角三角形，即可得∠BCO=∠OBC=45°，已知点P为第一象限内抛物线上的一点,且∠PCB=45°，可得PC∥OB，所以P点的纵坐标为3，令y=3，解方程即可求得点...

如图，抛物线y=－x2+bx+c与x轴交于A(－1,0),B(5,0）两点，直线y=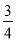－x+3与y轴交于点C，，与x轴交于点D.点P是x轴上方的抛物线上一动点，过点P作PF⊥x轴于点F，交直线CD于点E.设点P的横坐标为m。

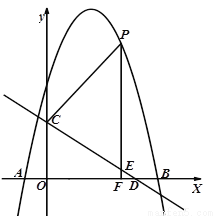
（1）求抛物线的解析式；（2）若PE=5EF,求m的值；（3）若点E′是点E关于直线PC的对称点、是否存在点P，使点E/落在y轴上？若存在，请直接写出相应的点P的坐标；若不存在，请说明理由。

(1)、y=－+4x+5；(2)、m=2或m=；(3)、， (4，5)， . 【解析】试题分析：(1)、利用待定系数法进行求解；(2)、首先设出点P、点E和点F的坐标，求出PE的长度，然后根据点E在点F的上方和下方两种情况分别进行计算；(3)、根据△CME和△COD相似来进行求解. 试题解析：(1)、将A、B两点的坐标代入得： 解得： ∴抛物线的解析式为：y=－+4x+5 ...

下列命题中，真命题是（　　）

A. 一组对边平行，另一组对边相等的四边形一定是等腰梯形

B. 对角线互相垂直的四边形是菱形

C. 顺次连结菱形各边中点所得的四边形是正方形

D. 四个内角均相等的四边形是矩形

D 【解析】选项A，一组对边平行，另一组对边相等的四边形不一定是等腰梯形；选项B，对角线互相垂直的平行四边形是菱形；选项C，顺次连结菱形各边中点所得的四边形是矩形；选项D，四个内角均相等的四边形是矩形．故选D．

已知：点P、Q是△ABC的边BC上的两个点，且BP=PQ=QC=AP=AQ，∠BAC的度数是（       ）

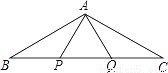
A. 100° B. 120° C. 130° D. 150°

B 【解析】∵PQ=AP=AQ， ∴∠APQ=∠PAQ=∠AQP=60°， 又∵AP=BP， ∴∠B=∠PAB，∠APQ=∠B＋∠PAB=60°， ∴∠B=∠PAB=30° ，同理∠QAC=∠C=30°， ∴∠BAC=∠PAQ＋∠PAB＋∠QAC=120°． 故选B.

如图是琳琳6个装好糖果的礼包盒，每盒上面的数字代表这盒礼包实际装有的糖果数量．她把其中的5盒送给好朋友小芬和小红，自己留下1盒．已知送的都是整盒，包装没拆过，送给小芬的糖果数量是小红的2倍，则琳琳自己留下的这盒有糖果（　　）

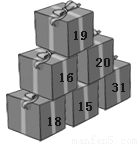
A. 15粒 B. 18粒 C. 20粒 D. 31粒

C 【解析】6个礼包盒一共有糖果：19+16+20+18+15+31=119（粒）， （1）119-19=100（粒），因为100÷3=33…1，所以琳琳自己留下的这盒糖果不是19粒； （2）119-16=103（粒），因为103÷3=34…1，所以琳琳自己留下的这盒糖果不是16粒； （3）119-20=99（粒），因为99÷3=33，所以琳琳送给小芬和小红的糖果的总量是9...