
科目: 来源:广西岑溪市2018届九年级上学期期中抽考数学试卷 题型:填空题
一条抛物线的顶点是A(2,1),且经过点B(1,0),则该抛物线的函数表达式是_____.
(或) 【解析】设抛物线解析式为y=a(x-2)2+1, 把B(1,0)代入得a+1=0,解得a=-1, 所以抛物线解析式为y=-(x-2)2+1,即y=-x2+4x-3 故答案为: (或y=-x2+4x-3).查看答案和解析>>
科目: 来源:广西岑溪市2018届九年级上学期期中抽考数学试卷 题型:填空题
已知P是线段AB上一点,且AP:PB=2:5,则AB:PB=_____.
7∶5 【解析】∵P是线段AB上一点,且AP:PB=2:5, ∴AB:PB=(2+5):5=7:5. 故答案为:7∶5.查看答案和解析>>
科目: 来源:广西岑溪市2018届九年级上学期期中抽考数学试卷 题型:填空题
如图是二次函数y=ax2+bx+c的部分图象,由图象可知方程ax2+bx+c=0的解是_________.
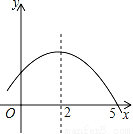
查看答案和解析>>
科目: 来源:广西岑溪市2018届九年级上学期期中抽考数学试卷 题型:解答题
请直接写出二次函数y=(x﹣1)2+2图象的开口方向、对称轴和顶点坐标.
开口向上;对称轴是:直线;顶点坐标是 . 【解析】试题分析:根据题目中的函数解析式,可以直接写出该函数图象的开口方向、对称轴和顶点坐标. 试题解析: :∵y=(x-1)2+2, ∴该函数的开口向上,对称轴是直线x=1,顶点坐标为(1,2).查看答案和解析>>
科目: 来源:广西岑溪市2018届九年级上学期期中抽考数学试卷 题型:解答题
已知y与x成反比例,且当x=2时,y=﹣3,求当x=﹣1时,y的值.
6. 【解析】试题分析:设y= ,将x=2时,y=-3代入求出k的值得到反比例函数解析式,再把x=-1代入即可求出对应y的值. 试题解析: 设,依题意得: , ∴ , ∴与之间的函数关系式为: , 把代入得: , 即:当时, .查看答案和解析>>
科目: 来源:广西岑溪市2018届九年级上学期期中抽考数学试卷 题型:解答题
如图所示,小华站在距离路灯的灯杆(AB)5m的C点处,测得她在路灯灯光下的影长(CD)为2.5m,已知小华的身高(EC)是1.6m,求路灯的灯杆AB的高度.
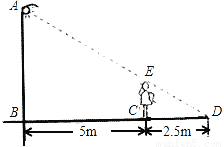
查看答案和解析>>
科目: 来源:广西岑溪市2018届九年级上学期期中抽考数学试卷 题型:解答题
已知:如图,D是△ABC的边AB上一点,且∠B=∠ACD.求证:AC2=AD•AB.
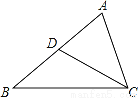
查看答案和解析>>
科目: 来源:广西岑溪市2018届九年级上学期期中抽考数学试卷 题型:解答题
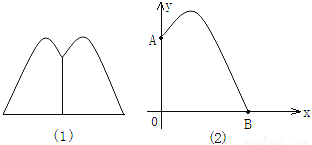
某地要建造一个圆形喷水池,在水池中央垂直于水面安装一个花形柱子OA,O恰好在水面中心,安装在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过OA的任一平面上,抛物线的形状如图(1)和(2)所示,建立直角坐标系,水流喷出的高度y(米)与水平距离x(米)之间的关系式是y=﹣x2+2x+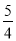 ,请回答下列问题.
,请回答下列问题.
(1)柱子OA的高度为多少米?
(2)喷出的水流距水平面的最大高度是多少?
(3)若不计其他因素,水池的半径至少要多少米,才能使喷出的水流不至于落在池外?
查看答案和解析>>
科目: 来源:广西岑溪市2018届九年级上学期期中抽考数学试卷 题型:解答题
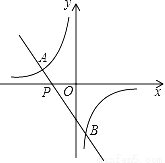
已知:如图,一次函数y=﹣2x﹣3的图象与反比例函数y=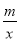 (m≠0)的图象相交于点A(﹣2,1)和点B.
(m≠0)的图象相交于点A(﹣2,1)和点B.
(1)求反比例函数的解析式;
(2)求点B的坐标;
(3)根据图象回答:当x在什么范围内取值时,一次函数的函数值小于反比例函数的函数值?
查看答案和解析>>
科目: 来源:广西岑溪市2018届九年级上学期期中抽考数学试卷 题型:解答题
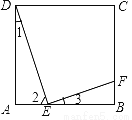
如图,E是正方形ABCD的边AB上的动点,但始终保持EF⊥DE交BC于点F.
(1)求证:△ADE∽△BEF;
(2)若正方形的边长为4,设AE=x,BF=y,求y与x之间的函数解析式;
(3)当x取何值时,y有最大值?并求出这个最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com