
科目: 来源:2017年湖北省宜昌市中考数学模拟试卷(三) 题型:解答题
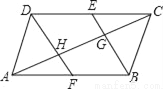
如图,在平行四边形ABCD中,∠ABC和∠ADC的平分线分别交对边于点E、F,交四边形的对角线AC于点G、H.求证:AH=CG.
查看答案和解析>>
科目: 来源:2017年湖北省宜昌市中考数学模拟试卷(三) 题型:解答题
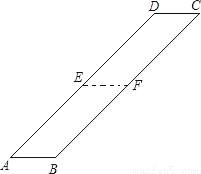
如图,平行四边形ABCD中,E、F分别是边AD,BC的中点.张老师请同学们将纸条的下半部分即平行四边形ABFE沿EF翻折,得到一个V字形图案.
(1)请你在原图中画出翻折后的图形平行四边形A′B′FE(用尺规作图,不写画法,保留作图痕迹)
(2)已知∠A=63°,求∠B′FC的大小.
查看答案和解析>>
科目: 来源:2017年湖北省宜昌市中考数学模拟试卷(三) 题型:解答题
某施工队挖掘一条长96米的隧道,开工后每天比原计划多挖2米,结果提前4天完成任务,原计划每天挖多少米?
原计划每天挖6米 【解析】试题分析:根据相等关系式“原计划工作天数-实际工作时间=4”列出方程求解即可. 试题解析:设原计划每天挖x米,根据题意得 解得 x1=6,x2=﹣8.(不合题意,舍去) 经检验,x1=6,x2=﹣8都是所列方程的根. 但x2=﹣8不合题意,舍去. ∴x=6. 答:原计划每天挖6米.查看答案和解析>>
科目: 来源:2017年湖北省宜昌市中考数学模拟试卷(三) 题型:解答题
某课外学习小组在设计一个长方形时钟钟面时,欲使长方形的宽为20厘米,时钟的中心在长方形对角线的交点上,数字2在长方形的顶点上,数字3、6、9、12标在所在边的中点上,如图所示。
(1)问长方形的长应为多少?
(2)请你在长方框上点出数字1的位置,并说明确定该位置的方法;
(3)请你在长方框上点出钟面上其余数字的位置,并写出相应的数字(说明:要画出必要的、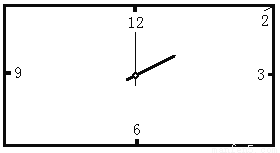
查看答案和解析>>
科目: 来源:2017年湖北省宜昌市中考数学模拟试卷(三) 题型:解答题
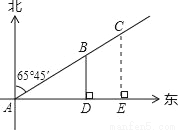
如图,一条渔船某时刻在位置A观测灯塔B、C(灯塔B距离A处较近),两个灯塔恰好在北偏东65°45′的方向上,渔船向正东方向航行l小时45分钟之后到达D点,观测到灯塔B恰好在正北方向上,已知两个灯塔之间的距离是12海里,渔船的速度是16海里/时,又知在灯塔C周围18.6海里内有暗礁,问这条渔船按原来的方向继续航行,有没有触礁的危险?
查看答案和解析>>
科目: 来源:2017年湖北省宜昌市中考数学模拟试卷(三) 题型:解答题
如图,AB切⊙O于点B,OA交⊙O于C点,过C作DC⊥OA交AB于D,且BD:AD=1:2.
(1)求∠A的正切值;
(2)若OC=1,求AB及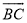 的长.
的长.
查看答案和解析>>
科目: 来源:2017年湖北省宜昌市中考数学模拟试卷(三) 题型:解答题
学校书法兴趣小组准备到文具店购买A、B两种类型的毛笔,文具店的销售方法是:一次性购买A型毛笔不超过20支时,按零售价销售;超过20支时,超过部分每支比零售价低0.4元,其余部分仍按零售价销售.一次性购买B型毛笔不超过15支时,按零售价销售;超过15支时,超过部分每支比零售价低0.6元,其余的部分仍按零售价销售.
(1)如果全组共有20名同学,若每人各买1支A型毛笔和2支B型毛笔,共支付145元;若每人各买2支A型毛笔和1支B型毛笔,共支付129元,这家文具店的A、B型毛笔的零售价各是多少?
(2)为了促销,该文具店对A型毛笔除了原来的销售方法外,同时又推出了一种新的销售方法:无论购买多少支,一律按原零售价(即(1)中所求得的A型毛笔的零售价)90%出售.现要购买A型毛笔a支(a>40),在新的销售方法和原来的销售方法中,应选择哪种方法购买花钱较少并说明理由.
(1)这家文具店A型毛笔的零售价为每支2元,B型毛笔的零售价为每支3元(2)用原来的方法购买花钱少 【解析】试题分析:(1)设这家文具店的A型毛笔零售价为每支x元,B型毛笔的零售价为每支y元,根据题中的数量关系,全组共有20名同学,若每人各买1支型毛笔和2支B型毛笔,共支付145元,列出方程20x+15y+25(y-0.6)=145,每人各买2支A型毛笔和1支B型毛笔,共支付129元列出20...查看答案和解析>>
科目: 来源:2017年湖北省宜昌市中考数学模拟试卷(三) 题型:解答题
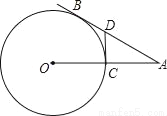
如图,已知平行四边形ABCD及四边形外一直线l,四个顶点A、B、C、D到直线l的距离分别为a、b、c、d.
(1)观察图形,猜想得出a、b、c、d满足怎样的关系式?证明你的结论.
(2)现将l向上平移,你得到的结论还一定成立吗?请分情况写出你的结论.
查看答案和解析>>
科目: 来源:2017年湖北省宜昌市中考数学模拟试卷(三) 题型:解答题
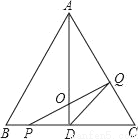
如图,在△ABC中,已知AB=BC=CA=4cm,AD⊥BC于D.点P、Q分别从B、C两点同时出发,其中点P沿BC向终点C运动,速度为1cm/s;点Q沿CA、AB向终点B运动,速度为2cm/s,设它们运动的时间为x(s).
(1)当x= 时,PQ⊥AC,x= 时,PQ⊥AB;
(2)设△PQD的面积为y(cm2),当0<x<2时,求y与x的函数关系式为 ;
(3)当0<x<2时,求证:AD平分△PQD的面积;
(4)探索以PQ为直径的圆与AC的位置关系,请写出相应位置关系的x的取值范围(不要求写出过程).
查看答案和解析>>
科目: 来源:山东省临朐县沂山风景区2017-2018学年八年级上期末模拟数学试卷 题型:填空题
如果一个三角形的三个内角都相等,那么这个三角形的形状是________.
等边三角形 【解析】【解析】 ∵一个三角形的三个内角都相等,∴每个角等于60°,∴这个三角形的形状是等边三角形.故答案为:等边三角形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com