
科目: 来源:2017年辽宁省中考数学二模试卷 题型:解答题
先化简,再求值:  ,其中x=
,其中x=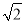 ﹣1.
﹣1.
查看答案和解析>>
科目: 来源:2017年辽宁省中考数学二模试卷 题型:解答题
已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中, 每个小正方形的边长是1个单位长度)
(1)画出△ABC向下平移4个单位得到的△A1B1C1,并直接写出C1点的坐标;
(2)以点B为位似中心,在网格中画出△A2BC2,使△A2BC2与△ABC位似,且位似比为2︰1,并直接写出C2点的坐标及△A2BC2的面积.

查看答案和解析>>
科目: 来源:2017年辽宁省中考数学二模试卷 题型:解答题
某小型企业实行工资与业绩挂钩制度,工人工资分为A、B、C、D四个档次.小明对该企业三月份工人工资进行调查,并根据收集到的数据,绘制了如下尚不完整的统计表与扇形统计图.
档次 | 工资(元) | 频数(人) | 频率 |
A | 3000 | 20 | |
B | 2800 | 0.30 | |
C | 2200 | ||
D | 2000 | 10 |
根据上面提供的信息,回答下列问题:
(1)求该企业共有多少人?
(2)请将统计表补充完整;
(3)扇形统计图中“C档次”的扇形所对的圆心角是 度.
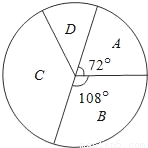
查看答案和解析>>
科目: 来源:2017年辽宁省中考数学二模试卷 题型:解答题
某商场为了吸引顾客,设计了一种促销活动.在一个不透明的箱子里放有4个完全相同的小球,球上分别标有“0元”、“10元”、“30元”、“50元”的字样.规定:顾客在本商场同一日内,消费每满300元,就可以从箱子里先后摸出两个球(每次只摸出一个球,第一次摸出后不放回).商场根据两个小球所标金额之和返还相应价格的购物券,可以重新在本商场消费.某顾客消费刚好满300元,则在本次消费中:
(1)该顾客至少可得 元购物券,至多可得 元购物券;
(2)请用画树状图或列表法,求出该顾客所获购物券的金额不低于50元的概率.
(1)10;80 (2) 【解析】分析:(1)根据题意即可求得该顾客至少可得的购物券,至多可得的购物券的金额;(2)首先根据题意列出表格,然后由表格求得所有等可能的结果与该顾客所获购物券的金额不低于50元的情况,再利用概率公式求解即可求得答案. 本题解析:.(1)10,80;(2) (2)方法一:树状图法: 方法二:列表法: 0 10 30 ...查看答案和解析>>
科目: 来源:2017年辽宁省中考数学二模试卷 题型:解答题
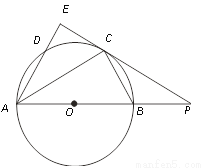
如图,在△ABC中,∠BAC=30°,以AB为直径的⊙O经过点C.过点C作⊙O的切线交AB的延长线于点P.点D为圆上一点,且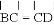 ,弦AD的延长线交切线PC于点E,连接BC.
,弦AD的延长线交切线PC于点E,连接BC.
(1)判断OB和BP的数量关系,并说明理由;
(2)若⊙O的半径为2,求AE的长.
查看答案和解析>>
科目: 来源:2017年辽宁省中考数学二模试卷 题型:解答题
暴雨过后,某地遭遇山体滑坡,武警总队派出一队武警战士前往抢险. 半小时后,第二队前去支援,平均速度是第一队的1.5倍,结果两队同时到达.已知抢险队的出发地与灾区的距离为90千米,两队所行路线相同,问两队的平均速度分别是多少?
第一队的平均速度是60千米/时,第二队的平均速度是90千米/时 【解析】试题分析:设第一队的平均速度是x千米/时,则第二队的平均速度是1.5x千米/时.根据半小时后,第二队前去支援,结果两队同时到达,即第一队与第二队所用时间的差是小时,即可列方程求解. 设第一队的平均速度是x千米/时,则第二队的平均速度是1.5x千米/时,根据题意得: ,解得x=60 经检验,x=60是所列...查看答案和解析>>
科目: 来源:2017年辽宁省中考数学二模试卷 题型:解答题
南中国海是中国固有领海,我渔政船经常在此海域执勤巡察.一天我渔政船停在小岛A北偏西37°方向的B处,观察A岛周边海域.据测算,渔政船距A岛的距离AB长为10海里.此时位于A岛正西方向C处的我渔船遭到某国军舰的袭扰,船长发现在其北偏东50°的方向上有我方渔政船,便发出紧急求救信号.渔政船接警后,立即沿BC航线以每小时30海里的速度前往救助,问渔政船大约需多少分钟能到达渔船所在的C处?

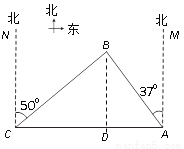
查看答案和解析>>
科目: 来源:2017年辽宁省中考数学二模试卷 题型:解答题
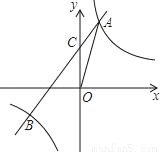
如图,反比例函数y=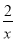 的图象与一次函数y=kx+b的图象交于点A(m,2),点B(﹣2,n ),一次函数图象与y轴的交点为C.
的图象与一次函数y=kx+b的图象交于点A(m,2),点B(﹣2,n ),一次函数图象与y轴的交点为C.
(1)求一次函数解析式;
(2)求C点的坐标;
(3)求△AOB的面积.
查看答案和解析>>
科目: 来源:2017年辽宁省中考数学二模试卷 题型:解答题
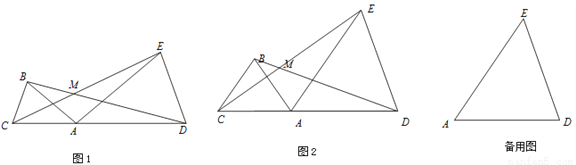
已知:点C、A、D在同一条直线上,∠ABC=∠ADE=α,线段 BD、CE交于点M.
(1)如图1,若AB=AC,AD=AE
①问线段BD与CE有怎样的数量关系?并说明理由;②求∠BMC的大小(用α表示);
(2)如图2,若AB= BC=kAC,AD =ED=kAE 则线段BD与CE的数量关系为 ,∠BMC= (用α表示);
(3)在(2)的条件下,把△ABC绕点A逆时针旋转180°,在备用图中作出旋转后的图形(要求:尺规作图,不写作法,保留作图痕迹),连接 EC并延长交BD于点M.则∠BMC= (用α表示).
查看答案和解析>>
科目: 来源:2017年辽宁省中考数学二模试卷 题型:解答题
已知抛物线y=ax2-2ax+c与y轴交于C点,与x轴交于A、B两点,点A的坐标是(-1,0),O是坐标原点,且OC=3OA.
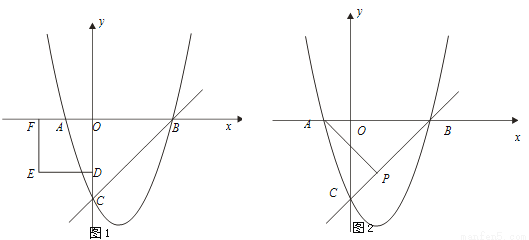
(1)求抛物线的函数表达式;
(2)直接写出直线BC的函数表达式;
(3)如图1,D为y轴的负半轴上的一点,且OD=2,以OD为边作正方形ODEF.将正方形ODEF以每秒1个单位的速度沿x轴的正方向移动,在运动过程中,设正方形ODEF与△OBC重叠部分的面积为s,运动的时间为t秒(0<t≤2).
求:①s与t之间的函数关系式;
②在运动过程中,s是否存在最大值?如果存在,直接写出这个最大值;如果不存在,请说明理由.
(4)如图2,点P(1,k)在直线BC上,点M在x轴上,点N在抛物线上,是否存在以A、M、N、P为顶点的平行四边形?若存在,请直接写出M点坐标;若不存在,请说明理由.
(1)y=x2-2x-3 ; (2)直线BC的函数表达式为y=x-3; (3)① ②当t =2秒时,S有最大值,最大值为. (4)存在符合条件的点M,且坐标为M 1(-,),M2(,), M3(,),M4(,) 【解析】分析:(1)先由OC、OA的数量关系确定点C的坐标,然后利用待定系数法可求出抛物线的解析式; (2)由(1)的抛物线解析式可得点B的坐标,结合点C的坐...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com