
科目: 来源:河南省禹州市2017-2018学年九年级上学期期中考试数学试卷 题型:填空题
一元二次方程a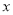 2+b
2+b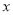 +c=0的两根是-
+c=0的两根是-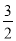 、-1,则二次函数y=a
、-1,则二次函数y=a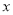 2+b
2+b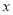 +c的图象与
+c的图象与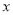 轴的两个交点间的距离为 .
轴的两个交点间的距离为 .
查看答案和解析>>
科目: 来源:河南省禹州市2017-2018学年九年级上学期期中考试数学试卷 题型:填空题
已知抛物线y=a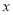 2+b
2+b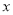 +c(a>0)的对称轴为直线
+c(a>0)的对称轴为直线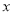 =1,且经过点(-1,y1)、(2,y2),试比较y1和y2的大小:y1 y2(填“>”“<”“=”).
=1,且经过点(-1,y1)、(2,y2),试比较y1和y2的大小:y1 y2(填“>”“<”“=”).
查看答案和解析>>
科目: 来源:河南省禹州市2017-2018学年九年级上学期期中考试数学试卷 题型:填空题
如图AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=4 ,则阴影部分图形的面积为 .
,则阴影部分图形的面积为 .

查看答案和解析>>
科目: 来源:河南省禹州市2017-2018学年九年级上学期期中考试数学试卷 题型:解答题
解下列方程:(1)3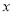 (
(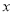 +1)=5(
+1)=5(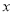 +1)
+1)
(2)5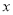 (
(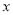 +1)=7
+1)=7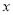 +1
+1
查看答案和解析>>
科目: 来源:河南省禹州市2017-2018学年九年级上学期期中考试数学试卷 题型:解答题
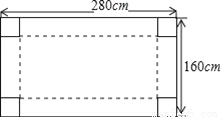
我国水资源比较缺乏,人均水量约为世界人均水量的四分之一,其中西北地区缺水尤为严重.一村民为了蓄水,他把一块矩形白铁皮四个角各切去一个同样大小的小正方形后制作一个无盖水箱用于接雨水.已知白铁皮的长为280cm,宽为160cm(如图).
(1)若水箱的底面积为16000cm2,请求出切去的小正方形边长;
(2)对(1)中的水箱,若盛满水,这时水量是多少升?(注:1升水=1000cm3水)
查看答案和解析>>
科目: 来源:河南省禹州市2017-2018学年九年级上学期期中考试数学试卷 题型:解答题
如图,在正方形网络中,△ABC各顶点都在格点上,点A,C的坐标分别为(-5,1)、(-1,4),结合所给的平面直角坐标系解答下列问题:
画出△ABC关于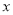 轴对称的△A1B1C1;
轴对称的△A1B1C1;
画出△ABC关于原点O对称的△A2B2C2;
点C1的坐标是 ;点C2的坐标是 ;
试判断:△A1B1C1与△A2B2C2是否关于y轴对称?(只需写出判断结果)
查看答案和解析>>
科目: 来源:河南省禹州市2017-2018学年九年级上学期期中考试数学试卷 题型:解答题
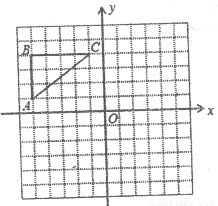
如图,将等腰△ABC绕顶点B逆时针方向旋转40°得到△A1BC1,AB与A1C1相交于点D,AC与A1C1、BC1分别交于点E、F.
求证:ΔBCF≌ΔBA1D.
当∠C=40°时,请你证明四边形A1BCE是菱形.
(1)详见解析;(2)详见解析. 【解析】试题分析:(1)根据旋转的性质,得出A1B=AB=BC,∠A=∠A1=∠C,∠A1BD=∠CBC1,再根据ASA即可判定△BCF≌△BA1D; (2)根据∠C=40°,△ABC是等腰三角形,即可得出∠A=∠C1=∠C=40°,进而得到∠C1=∠CBF,∠A=∠A1BD,由此可判定A1E∥BC,A1B∥CE,进而得到四边形A1BCE是平行四边形,...查看答案和解析>>
科目: 来源:河南省禹州市2017-2018学年九年级上学期期中考试数学试卷 题型:解答题
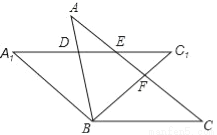
“圆材埋壁”是我国古代著名的数学著作《九章算数》中的一个问题,”今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何? 用现在的数学语言表述是:如图,CD为⊙O的直径,弦AB⊥CD垂足为E,CE=1寸,AB=10寸,求直径CD的长”.
查看答案和解析>>
科目: 来源:河南省禹州市2017-2018学年九年级上学期期中考试数学试卷 题型:解答题
如图,已知直线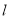 与⊙O相离,OA⊥
与⊙O相离,OA⊥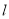 于点A,交⊙O于点P,点B是⊙O上一点,连接BP并延长,交直线
于点A,交⊙O于点P,点B是⊙O上一点,连接BP并延长,交直线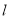 于点C,使得AB=AC.
于点C,使得AB=AC.
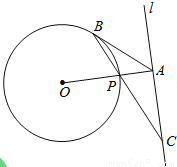
(1)求证:AB是⊙O的切线;
(2)若PC=2 ,OA=4,求⊙O的半径.
,OA=4,求⊙O的半径.
查看答案和解析>>
科目: 来源:河南省禹州市2017-2018学年九年级上学期期中考试数学试卷 题型:解答题
某片果园有果树80棵,现准备多种一些果树提高产量,但是如果多种树,那么树之间的距离和每棵树所受光照就会减少,单棵树的产量随之降低.若该果园每棵果树产果y(千克),增种果树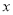 (棵),它们之间的函数关系如图所示.
(棵),它们之间的函数关系如图所示.
(1)求y与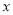 之间的函数关系式;
之间的函数关系式;
(2)当增种果树多少棵时,果园的总产量w(千克)最大?最大产量是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com