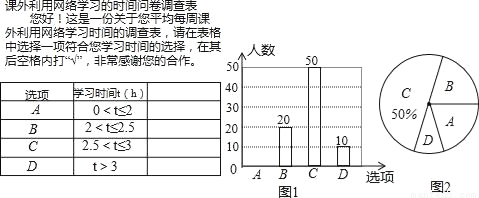
随着教育信息化的发展，学生的学习方式日益增多，教师为了指导学生有效利用网络进行学习，对学生进行了随机问卷调查（问卷调查表如图所示），并用调查结果绘制了图1、图2两幅统计图（均不完整），请根据统计图解答以下问题：

（1）本次接受问卷调查的学生共有　 　人，在扇形统计图中“D“选项所占的百分比为　 　；

（2）扇形统计图中，“B”选项所对应扇形圆心角为　 　度；

（3）请补全条形统计图；

（4）若该校共有1200名学生，请您估计该校学生课外利用网络学习的时间在“A”选项的有多少人？

（1）100，10%；（2）72；（3）补图见解析；（4）240人. 【解析】由条形统计图与扇形统计图获得的数据： 因为图（1）、图（2）中已知C选项的百分比与人数，由C选项的百分比=×100％求解； 先求出B选项的百分比，再利用扇形统计图的圆心角的度数=360°×B选项的百分比求解； （3）由（1）所得总人数求出B选项的人数即可作图； （4）先求出A选项的百分比即可...

某体育场看台的坡面AB与地面的夹角是37°，看台最高点B到地面的垂直距离BC为2.4米，看台正前方有一垂直于地面的旗杆DE，在B点用测角仪测得旗杆的最高点E的仰角为33°，已知测角仪BF的高度为1.2米，看台最低点A与旗杆底端D之间的距离为15米（C，A，D在同一条直线上）．

（1）求看台最低点A到最高点B的坡面距离AB；

（2）一面红旗挂在旗杆上，固定红旗的上下两个挂钩G、H之间的距离为1.2米，下端挂钩H与地面的距离为1米，要求用30秒的时间将红旗升到旗杆的顶端，求红旗升起的平均速度（计算结果保留两位小数）（sin37°≈0.6，cos37°≈0.8，tan37°≈0.75，sin33°≈0.54，cos33°≈0.84，tan33°≈0.65）

（1）4米；（2）红旗升起的平均速度为0.45米/秒． 【解析】（1）根据正弦的定义计算即可； （2）作FP⊥ED于P，根据正切的定义求出AC，根据正切的概念求出EP，计算即可． 【解析】 （1）在Rt△ABC中，AB==4米； （2）AC==3.2米，则CD=3.2+15=18.5米， 作FP⊥ED于P， ∴FP=CD=18.5， ∴EP=FP×tan...

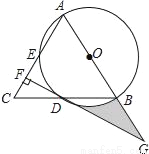
如图，在△ABC中，AB=AC，以AB为直径的⊙O分别交线段BC，AC于点D，E，过点D作DF⊥AC，垂足为F，线段FD，AB的延长线相交于点G．

（1）求证：DF是⊙O的切线；

（2）若CF=2，DF=2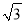，求图中阴影部分的面积．

（1）证明见解析；（2）. 【解析】（1）连接AD、OD，由AB为直径可得出点D为BC的中点，由此得出OD为△BAC的中位线，再根据中位线的性质即可得出OD⊥DF，从而证出DF是⊙O的切线； （2）CF=1，DF=，通过解直角三角形得出CD=2、∠C=60°，从而得出△ABC为等边三角形，再利用分割图形求面积法即可得出阴影部分的面积． （1）证明：连接AD、OD，如图所示． ...

某工厂生产一种合金薄板（其厚度忽略不计）这些薄板的形状均为正方形，边长（单位：cm）在5～50之间，每张薄板的成本价（单位：元）与它的面积（单位：cm2）成正比例，每张薄板的出厂价（单位：元）由基础价和浮动价两部分组成，（即出厂价=基础价+浮动价）其中基础价与薄板的大小无关，是固定不变的，浮动价与薄板的边长x成正比例，在营销过程中得到了表格中的数据，已知出厂一张边长为40cm的薄板，获得利润是26元．（利润=出厂价﹣成本价）

薄板的边长（cm）	20	30
出厂价（元/张）	50	70

（1）求一张薄板的出厂价y与边长x之间满足的函数关系式；

（2）求一张薄板的利润p与边长x之间的函数关系式；

（3）若一张薄板的利润是34元，且成本最低，此时薄板的边长为多少？当薄板的边长为多少时，所获利润最大，求出这个最大值．

（1）y=2x+10；（2）p=﹣x2+2x+10；（3）当薄板的边长为25cm时，所获利润最大，最大值35元． 【解析】（1）利用待定系数法求一次函数解析式即可得出答案； （2）首先假设一张薄板的利润为p元，它的成本价为mx2元，由题意，得：p=y-mx2，进而得出m的值，求出函数解析式即可； （3）利用二次函数的最值公式求出二次函数的最值即可． 【解析】 （1）设一张薄板的边...

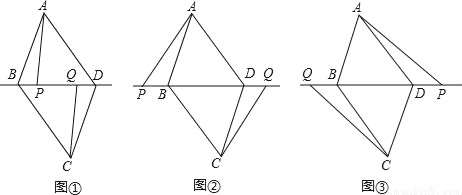
在?ABCD中，点P和点Q是直线BD上不重合的两个动点，AP∥CQ，AD=BD．

（1）如图①，求证：BP+BQ=BC；

（2）请直接写出图②，图③中BP、BQ、BC三者之间的数量关系，不需要证明；

（3）在（1）和（2）的条件下，若DQ=2，DP=6，则BC=　 　．

（1）证明见解析；（2）答案见解析；（3）4或8． 【解析】（1）根据平行四边形的性质证明△ADP≌△CBQ，得BQ=PD，由AD=BD=BC得：BC=BD=BP+PD=BP+BQ； （2）图②，证明△ABP≌△CDQ，得PB=DQ，根据线段的和得结论； 图③，证明△ADP≌△CBQ，得PD=BQ，同理得出结论； （3）分别代入图①和图②条件下的BC，计算即可． 【解...

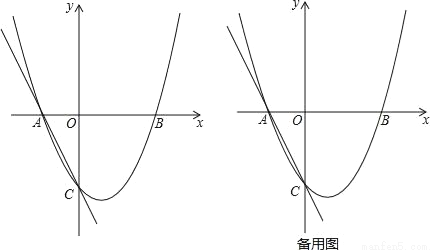
如图，二次函数y=ax2+bx+c的图象交x轴于A（﹣1，0），B（2，0），交y轴于C（0，﹣2），过A，C画直线．

（1）求二次函数的解析式；

（2）点P在x轴正半轴上，且PA=PC，求OP的长；

（3）点M在二次函数图象上，以M为圆心的圆与直线AC相切，切点为H．

①若M在y轴右侧，且△CHM∽△AOC（点C与点A对应），求点M的坐标；

②若⊙M的半径为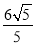，求点M的坐标．

（1）y=x2﹣x﹣2；（2）；（3）①M（1，﹣2），M′（， ）；②（2，0）或（﹣3，10）． 【解析】（1）根据与x轴的两个交点A、B的坐标，利设出两点法解析式，然后把点C的坐标代入计算求出a的值，即可得到二次函数解析式； （2）设OP=x，然后表示出PC、PA的长度，在Rt△POC中，利用勾股定理列式，然后解方程即可； （3）①根据相似三角形对应角相等可得∠MCH=∠C...

在下列选项中，具有相反意义的量是（ ）

A．收入20元与支出30元

B．上升了6米和后退了7米

C．卖出10斤米和盈利10元

D．向东行30米和向北行30米

A 【解析】 试题分析：收入20元与支出30元是一对具有相反意义的量.故选：A.

下列各式中，与（﹣a+1）2相等的是（　　）

A. a2﹣1 B. a2+1 C. a2﹣2a+1 D. a2+2a+1

C 【解析】因为（﹣a+1）2=a2-2a+1，故选D.

已知点A(m，1)与点B（5，n）关于原点对称，则m和n的值为

A. m=5，n=－1 B. m=－5，n=1 C. m=－1，n=－5 D. m=－5，n=－1

D 【解析】试题分析：根据原点对称的点的特点，横纵坐标均互为相反数，可知m=-5，n=-1. 故选：D.

已知，则的值为（　　）

A. B. C. ﹣2 D. 2

C 【解析】∵，∴，∴， 故选C.