练习册

  • 练习册
  • 试题
    相关习题
     0  320153  320161  320167  320171  320177  320179  320183  320189  320191  320197  320203  320207  320209  320213  320219  320221  320227  320231  320233  320237  320239  320243  320245  320247  320248  320249  320251  320252  320253  320255  320257  320261  320263  320267  320269  320273  320279  320281  320287  320291  320293  320297  320303  320309  320311  320317  320321  320323  320329  320333  320339  320347  366461 

    科目： 来源：北京八十五中2017-2018学年上期期末八年级数学试卷 题型：单选题

    一个多边形每个外角都等于36°，则这个多边形是几边形（ ）

    A．7 B．8 C．9 D．10

    D 【解析】 试题分析：多边形的外角和是360°，又有多边形的每个外角都等于36°，所以可以求出多边形外角的个数，进而得到多边形的边数． 【解析】 这个多边形的边数是：=10．故答案是D．

    查看答案和解析>>

    科目： 来源：北京八十五中2017-2018学年上期期末八年级数学试卷 题型：单选题

    如图，已知△ABC中，∠A=75°，则∠1+∠2=( )

    A. 335°° B. 255° C. 155° D. 150°

    B 【解析】∵∠A+∠B+∠C=180°，∠A=75°， ∴∠B+∠C=180°﹣∠A=105°． ∵∠1+∠2+∠B+∠C=360°， ∴∠1+∠2=360°﹣105°=255°． 故选B．

    查看答案和解析>>

    科目： 来源：北京八十五中2017-2018学年上期期末八年级数学试卷 题型：单选题

    下列从左到右的运算是因式分解的是( )

    A. 2a2﹣2a+1=2a（a﹣1）+1 B. （x﹣y）（x+y）=x2﹣y2

    C. 9x2﹣6x+1=（3x﹣1）2 D. x2+y2=（x﹣y）2+2xy

    C 【解析】A.没把一个多项式转化成几个整式积的形式，故A错误； B、是整式的乘法，故B错误； C、把一个多项式转化成几个整式积的形式，故C正确； D、没把一个多项式转化成几个整式积的形式，故D错误； 故选：C．

    查看答案和解析>>

    科目： 来源：北京八十五中2017-2018学年上期期末八年级数学试卷 题型：单选题

    若等腰三角形的两边长分别为6和8，则周长为（　　）

    A. 20或22 B. 20 C. 22 D. 无法确定

    A 【解析】若6是腰长，则三角形的三边分别为6、6、8， 能组成三角形， 周长=6+6+8=20， 若6是底边长，则三角形的三边分别为6、8、8， 能组成三角形， 周长=6+8+8=22， 综上所述，三角形的周长为20或22． 故选A．

    查看答案和解析>>

    科目： 来源：北京八十五中2017-2018学年上期期末八年级数学试卷 题型：单选题

    已知：如图，∠1＝∠2，则不一定能使△ABD≌△ACD的条件是 （ ）

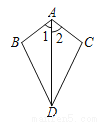
    A. AB＝AC B. BD＝CD C. ∠B＝∠C D. ∠BDA＝∠CDA

    B 【解析】试题分析：利用全等三角形判定定理ASA，SAS，AAS对各个选项逐一分析即可得出答案． 【解析】 A、∵∠1=∠2，AD为公共边，若AB=AC，则△ABD≌△ACD（SAS）；故A不符合题意； B、∵∠1=∠2，AD为公共边，若BD=CD，不符合全等三角形判定定理，不能判定△ABD≌△ACD；故B符合题意； C、∵∠1=∠2，AD为公共边，若∠B=∠C，则△A...

    查看答案和解析>>

    科目： 来源：北京八十五中2017-2018学年上期期末八年级数学试卷 题型：单选题

    如图，已知∠MON=30°，点A1，A2，A3，…在射线ON上，点B1，B2，B3，…在射线OM上，△A1B1A2，△A2B2A3，△A3B3A4，…均为等边三角形，若OA1=2，则△A5B5A6的边长为( )

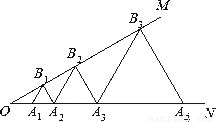
    A. 8 B. 16 C. 24 D. 32

    B 【解析】如图所示： ∵△A1B1A2是等边三角形， ∴A1B1=A2B1，∠3=∠4=∠12=60°， ∴∠2=120°， ∵∠MON=30°， ∴∠1=180°﹣120°﹣30°=30°， 又∵∠3=60°， ∴∠5=180°﹣60°﹣30°=90°， ∵∠MON=∠1=30°， ∴OA1=A1B1=1， ∴A2B1=1， ...

    查看答案和解析>>

    科目： 来源：北京八十五中2017-2018学年上期期末八年级数学试卷 题型：填空题

    科学家发现一种病毒的直径为0.0043微米，则用科学记数法表示为__________微米．

    4.3×10﹣34.3×10﹣3 【解析】0.0043=4.3×10﹣3．

    查看答案和解析>>

    科目： 来源：北京八十五中2017-2018学年上期期末八年级数学试卷 题型：填空题

    若一个三角形三个内角的度数之比为1：2：3，则这个三角形中的最大的角度是 ．

    90° 【解析】 试题分析：已知三角形三个内角的度数之比，可以设一份为k，根据三角形的内角和等于180°列方程求三个内角的度数，从而确定三角形的最大角的度数． 【解析】 设三个内角的度数分别为k，2k，3k． 则k+2k+3k=180°， 解得k=30°， 则2k=60°，3k=90°， 这个三角形最大的角等于90°． 故答案为：90°．

    查看答案和解析>>

    科目： 来源：北京八十五中2017-2018学年上期期末八年级数学试卷 题型：填空题

    计算（π﹣3.14）0+=__________．

    1010 【解析】：原式=1+9=10，

    查看答案和解析>>

    科目： 来源：北京八十五中2017-2018学年上期期末八年级数学试卷 题型：填空题

    若x2+mx+4是完全平方式，则m=_____．

    ±4 【解析】这里首末两项是2x和2这两个数的平方，那么中间一项为加上或减去2x和2积的2倍，依此求出m的值． 【解析】 ∵x2+mx+4是一个完全平方式， ∴这两个数2x和2， ∴mx=±2×2?x， 解得m=±4． 故答案为：±4．

    查看答案和解析>>

    同步练习册答案