
科目: 来源:重庆市校2018届九年级上学期期末模拟数学试卷 题型:单选题
在同一平面直角坐标系中,函数y=ax2+bx与y=bx+a的图象可能是( )
A. 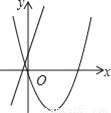 B.
B. 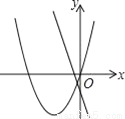 C.
C. 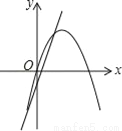 D.
D. 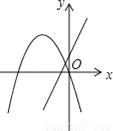
查看答案和解析>>
科目: 来源:重庆市校2018届九年级上学期期末模拟数学试卷 题型:单选题
如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( )
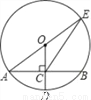
A. 2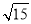 B. 8 C. 2
B. 8 C. 2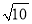 D. 2
D. 2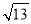
查看答案和解析>>
科目: 来源:重庆市校2018届九年级上学期期末模拟数学试卷 题型:单选题
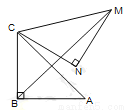
如图,在Rt△ABC中,∠ABC=90°,AB=BC=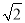 ,将△ABC绕点C逆时针旋转60°,得到△MNC,连结BM,则BM的长是( )
,将△ABC绕点C逆时针旋转60°,得到△MNC,连结BM,则BM的长是( )
A. 4 B. 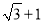 C.
C. 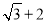 D.
D. 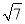
查看答案和解析>>
科目: 来源:重庆市校2018届九年级上学期期末模拟数学试卷 题型:单选题
从﹣3,﹣2,﹣1,0,1这五个数中,随机取出一个数,记为a,若a使得关于x的不等式组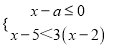 无解,且关于x的分式方程
无解,且关于x的分式方程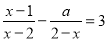 有整数解的概率为( )
有整数解的概率为( )
A. 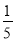 B.
B. 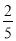 C.
C. 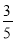 D.
D. 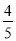
查看答案和解析>>
科目: 来源:重庆市校2018届九年级上学期期末模拟数学试卷 题型:填空题
关于x的一元二次方程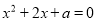 的一个根为1,则方程的另一根为______.
的一个根为1,则方程的另一根为______.
查看答案和解析>>
科目: 来源:重庆市校2018届九年级上学期期末模拟数学试卷 题型:填空题
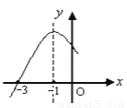
已知二次函数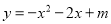 的部分图象如图所示,则一元二次方程
的部分图象如图所示,则一元二次方程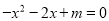 的解为:_____.
的解为:_____.
查看答案和解析>>
科目: 来源:重庆市校2018届九年级上学期期末模拟数学试卷 题型:填空题
若一个圆锥的底面圆半径为3 cm,母线长4cm,则它的侧面展开图的面积等于______ 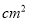 .
.
查看答案和解析>>
科目: 来源:重庆市校2018届九年级上学期期末模拟数学试卷 题型:填空题
对于平面内任意一个凸四边形ABCD,现从以下四个关系式: ①AB=CD;②AD=BC;③AB∥CD;④∠A=∠C中任取两个作为条件,能够得出这个四边形ABCD是平行四边形的概率是_______.
【解析】从四个条件中选两个共有六种可能:①②、①③、①④、②③、②④、③④, 其中只有①②、①③和③④可以判断四边形ABCD是平行四边形,所以能够得出这个四边形ABCD是平行四边形的概率是 .查看答案和解析>>
科目: 来源:重庆市校2018届九年级上学期期末模拟数学试卷 题型:填空题
如图,Rt△ABC中,∠A=90°,∠B=30°,AC=6,以A为圆心,AC长为半径画四分之一圆,则图中阴影部分面积为__________。(结果保留π)
查看答案和解析>>
科目: 来源:重庆市校2018届九年级上学期期末模拟数学试卷 题型:填空题
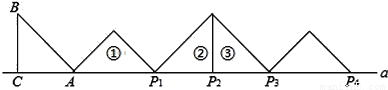
如图,等腰Rt△ABC中,∠ACB=90°,AC=BC=1,且AC边在直线a上,将△ABC绕点A顺时针旋转到位置①可得到点P1,此时AP1=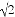 ;将位置①的三角形绕点P1顺时针旋转到位置②可得到点P2,此时AP2=
;将位置①的三角形绕点P1顺时针旋转到位置②可得到点P2,此时AP2=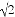 +1;将位置②的三角形绕点P2顺时针旋转到位置③可得到点P3时,AP3=
+1;将位置②的三角形绕点P2顺时针旋转到位置③可得到点P3时,AP3=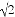 +2…按此规律继续旋转,直至得到点
+2…按此规律继续旋转,直至得到点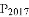 为止,则
为止,则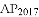 =________.
=________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com