
科目: 来源:2017年江苏省苏州市中考数学三模试卷 题型:解答题
化简: 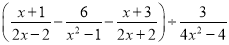 .
.
查看答案和解析>>
科目: 来源:2017年江苏省苏州市中考数学三模试卷 题型:解答题
解方程:  .
.
查看答案和解析>>
科目: 来源:2017年江苏省苏州市中考数学三模试卷 题型:解答题
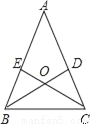
如图,△ABC中,D、E分别是AC、AB上的点,BD与CE交于点O.给出下列三个条件:
①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD.
(1)上述三个条件中,哪两个条件 可判定△ABC是等腰三角形(用序号写出所有情形);
(2)选择第(1)小题中的一种情形,证明△ABC是等腰三角形.
查看答案和解析>>
科目: 来源:2017年江苏省苏州市中考数学三模试卷 题型:解答题
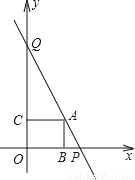
如图所示,直线y=﹣2x+8与两坐标轴分别交于P、Q两点,在线段PQ上有一点A,过点A分别作两坐标轴的垂线,垂足分别为B、C.若矩形ABOC的面积为5,求点A坐标.
查看答案和解析>>
科目: 来源:2017年江苏省苏州市中考数学三模试卷 题型:解答题
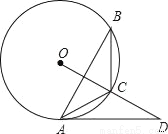
如图,△ABC内接于⊙O,过点A作⊙O的切线,交OC的延长线于点D,∠D=30°
(1)求∠B的度数;
(2)若OD⊥AB,BC=5,求AD的长.
查看答案和解析>>
科目: 来源:2017年江苏省苏州市中考数学三模试卷 题型:解答题
小明的家在某公寓楼AD内,他家的前面新建了一座大厦BC,小明想知道大厦的高度,但由于施工原因,无法测出公寓底部A与大厦底部C的直线距离,于是小明在他家的楼底A处测得大厦顶部B的仰角为60°,爬上楼顶D处测得大厦的顶部B的仰角为30°,已知公寓楼AD的高为60米,请你帮助小明计算出大厦的高度BC.
大厦的高度BC为90米. 【解析】试题分析:在图中有两个直角三角形,即和 若设 则根据30°、60°角的正切值可求得BC和BE,然后根据二者之间的关系,得到一个关于的方程解答即可. 试题解析:如图,由题意知:四边形ACED是矩形, ∴AC=DE,DA=EC=60米, 设DE=x, 在Rt△BDE中, 在Rt△BAC中, 即 解得: (米). ...查看答案和解析>>
科目: 来源:2017年江苏省苏州市中考数学三模试卷 题型:解答题
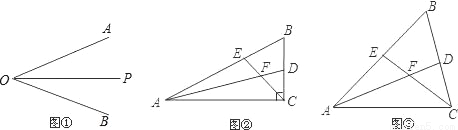
如图①,OP是∠AOB的平分线,请你利用该图形画一对以OP所在直线为对称轴的全等三角形.请你参考这个作全等三角形的方法,解答下列问题:
(1)如图②,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.请你判断并写出FE与FD之间的数量关系;
(2)如图③,在△ABC中,如果∠ACB不是直角,而(1)中的其它条件不变,请问,你在(1)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由.
查看答案和解析>>
科目: 来源:2017年江苏省苏州市中考数学三模试卷 题型:解答题
已知抛物线y=ax2+bx+c(a≠0)与x轴交于不同的两个点A(x1,0)和点B(x2,0)与y轴的正半轴交于点C,如果x1,x2是方程x2﹣2x﹣3=0的两个根(x1<x2),且图象经过点(2,3)
(1)求抛物线的解析式并画出图象
(2)x在什么范围内函数值y大于3且随x的增大而增大.
(3)设(1)中的抛物线顶点为D,在y轴上是否存在点P,使得DP+BP的和最小?若存在,求出这个最小值;若不存在,说明理由.
查看答案和解析>>
科目: 来源:2017年江苏省苏州市中考数学三模试卷 题型:解答题
将分别标有数字2,3,5的三张颜色、质地、大小完全一样的卡片背面朝上放在桌面上.
(1)随机抽取一张,求抽到奇数的概率;
(2)随机抽取一张作为个位上的数字(不放回),再抽取一张作为十位上的数字,能组成哪些两位数?并画树状图或列表求出抽取到的两位数恰好是35的概率.
(1)P(抽到奇数)=;(2)P(恰好抽到为35)= 【解析】试题分析:(1)先求出这组数中奇数的个数,再利用概率公式解答即可; (2)根据题意列举出能组成的数的个数及35的个数,再利用概率公式解答. 试题解析:(1)根据题意可得:有三张卡片,奇数只有“3和5”一张,故抽到奇数的概率P=; (2)根据题意可得:随机抽取一张作为个位上的数字(不放回),再抽取一张作为十位上的数...查看答案和解析>>
科目: 来源:2017年江苏省苏州市中考数学三模试卷 题型:解答题
苏州太湖养殖场计划养殖蟹和贝类产品,这两个品种的种苗的总投放量只有50吨,根据经验测算,这两个品种的种苗每投放一吨的先期投资,养殖期间的投资以及产值如下表(单位:万元/吨)
品种 | 先期投资 | 养殖期间投资 | 产值 |
贝类产品 | 0.9 | 0.3 | 0.33 |
蟹产品 | 0.4 | 1 | 2 |
养殖场受经济条件的影响,先期投资不超过36万元,养殖期间的投资不超过29万元,设贝类的种苗投放量为x吨,
(1)求x的取值范围;
(2)设这两个品种产出后的总产值为y(万元),试写出y与x之间的函数关系式,并求出当x等于多少时,y有最大值?最大值是多少?
(1)30≤x≤32;(2)当x=30时,y有最大值,且最大值是49.9万元. 【解析】试题分析:(1)可根据:养殖贝类产品的先期投资+养殖蟹产品的先期投资≤36;养殖贝类产品的养殖期间的投资+养殖蟹产品的养殖期间的投资≤29;列出不等式组,求出自变量的取值范围. (2)本题的等量关系是:养殖贝类产品的总产值+养殖蟹产品的总产值=两种产品的总产值.然后根据(1)中自变量的取值范围,求出符合...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com