
科目: 来源:2017年海南省海口市中考数学模拟试卷 题型:填空题
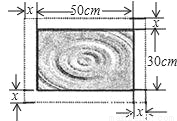
在一幅长50cm,宽30cm的风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示,如果要使整个规划土地的面积是1800cm2,设金色纸边的宽为xcm,那么x满足的方程为_____.
查看答案和解析>>
科目: 来源:2017年海南省海口市中考数学模拟试卷 题型:填空题
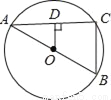
如图,AB是⊙O的直径,OD⊥AC于点D,BC=6cm,则OD=_____cm.
查看答案和解析>>
科目: 来源:2017年海南省海口市中考数学模拟试卷 题型:填空题
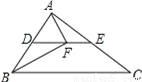
如图所示,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为_____.
查看答案和解析>>
科目: 来源:2017年海南省海口市中考数学模拟试卷 题型:解答题
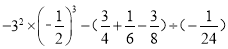
查看答案和解析>>
科目: 来源:2017年海南省海口市中考数学模拟试卷 题型:解答题
若不等式组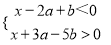 的解集为1<x<6,求a,b的值.
的解集为1<x<6,求a,b的值.
查看答案和解析>>
科目: 来源:2017年海南省海口市中考数学模拟试卷 题型:解答题
一个蓄水池有甲、乙两个进水管和一个丙排水管,单独开甲管6小时可注满水池;单独开乙管8小时可注满水池,单独开丙管9小时可将满池水排空,若先将甲、乙管同时开放2小时,然后打开丙管,问打开丙管后几小时可注满水池?
打开丙管后小时可注满水池. 【解析】设打开丙管后x小时可注满水池.等量关系为:甲注水量+乙注水量-丙排水量=1. 据此列出方程并解答. 【解析】 设打开丙管后x小时可注满水池, 由题意得,( +)(x+2)﹣x =1, 解这个方程, (x+2)﹣=1, 21x+42﹣8x=72, 13x=30, 解得x=. 答:打开丙管后小时可注满水池. ...查看答案和解析>>
科目: 来源:2017年海南省海口市中考数学模拟试卷 题型:解答题
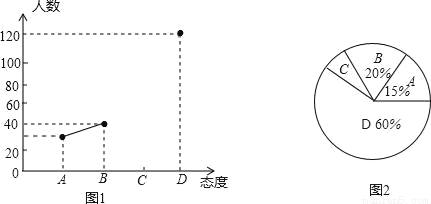
目前我市“校园手机”现象越来越受到社会关注,针对这种现象,重庆一中初三(1)班数学兴趣小组的同学随机调查了学校若干名家长对“中学生带手机”现象的态度(态度分为:A.无所谓;B.基本赞成;C.赞成;D.反对),并将调查结果绘制成频数折线统计图1和扇形统计图2(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了多少名中学生家长;
(2)求出图2中扇形C所对的圆心角的度数,并将图1补充完整;
(3)根据抽样调查结果,请你估计我校11000名中学生家长中有多少名家长持反对态度;
(4)在此次调查活动中,初三(1)班和初三(2)班各有2位家长对中学生带手机持反对态度,现从中选2位家长参加学校组织的家校活动,用列表法或画树状图的方法求选出的2人来自不同班级的概率.
查看答案和解析>>
科目: 来源:2017年海南省海口市中考数学模拟试卷 题型:解答题
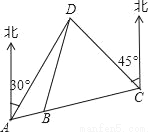
某市开展一项自行车旅游活动,线路需经A、B、C、D四地,如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向,在C地北偏西45°方向,C地在A地北偏东75°方向.且BC=CD=20km,问沿上述线路从A地到D地的路程大约是多少?(最后结果保留整数,参考数据:sin15°≈0.25,cos15°≈0.97,tan15°≈0.27, 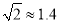 ,
, 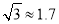 .)
.)
查看答案和解析>>
科目: 来源:2017年海南省海口市中考数学模拟试卷 题型:解答题
在平面直角坐标系中,O是坐标原点,?ABCD的顶点A的坐标为(﹣2,0),点D的坐标为(0,2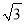 ),点B在x轴的正半轴上,点E为线段AD的中点.
),点B在x轴的正半轴上,点E为线段AD的中点.
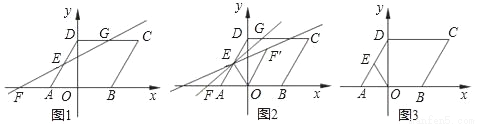
(Ⅰ)如图1,求∠DAO的大小及线段DE的长;
(Ⅱ)过点E的直线l与x轴交于点F,与射线DC交于点G.连接OE,△OEF′是△OEF关于直线OE对称的图形,记直线EF′与射线DC的交点为H,△EHC的面积为3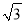 .
.
①如图2,当点G在点H的左侧时,求GH,DG的长;
②当点G在点H的右侧时,求点F的坐标(直接写出结果即可).
查看答案和解析>>
科目: 来源:2017年海南省海口市中考数学模拟试卷 题型:解答题
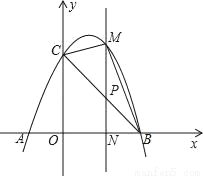
如图,已知抛物线y=﹣x2+2x+3与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,连接BC.
(1)求A,B,C三点的坐标;
(2)若点P为线段BC上一点(不与B,C重合),PM∥y轴,且PM交抛物线于点M,交x轴于点N,当△BCM的面积最大时,求△BPN的周长;
(3)在(2)的条件下,当△BCM的面积最大时,在抛物线的对称轴上存在一点Q,使得△CNQ为直角三角形,求点Q的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com