
科目: 来源:内蒙古2017年中考数学二模试卷 题型:解答题
如图,过正方形ABCD顶点B,C的⊙O与AD相切于点P,与AB,CD分别相交于点E,F,连接EF.
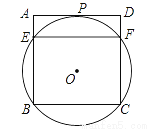
(1)求证:PF平分∠BFD;
(2)若tan∠FBC= 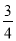 ,DF=
,DF=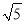 ,求EF的长.
,求EF的长.
查看答案和解析>>
科目: 来源:内蒙古2017年中考数学二模试卷 题型:解答题
某游泳馆普通票价20元/张,暑假为了促销,新推出两种优惠卡:
①金卡售价600元/张,每次凭卡不再收费.
②银卡售价150元/张,每次凭卡另收10元.
暑假普通票正常出售,两种优惠卡仅限暑假使用,不限次数.设游泳x次时,所需总费用为y元.
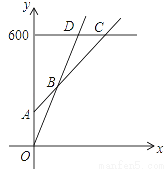
(1)分别写出选择银卡、普通票消费时,y与x之间的函数关系式;
(2)在同一坐标系中,若三种消费方式对应的函数图象如图所示,请求出点A、B、C的坐标;
(3)请根据函数图象,直接写出选择哪种消费方式更合算.
(1)银卡消费:y=10x+150,普通消费:y=20x;(2)A(0,150),B(15,300),C(45,600);(3)答案见解析. 【解析】试题分析:(1)根据银卡售价150元/张,每次凭卡另收10元,以及旅游馆普通票价20元/张,设游泳x次时,分别得出所需总费用为y元与x的关系式即可; (2)利用函数交点坐标求法分别得出即可; (3)利用(2)的点的坐标以及结合得出函...查看答案和解析>>
科目: 来源:内蒙古2017年中考数学二模试卷 题型:解答题
如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高2米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有25米的距离(B,F,C在一条直线上).
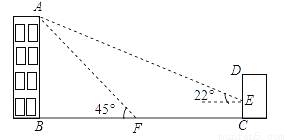
(1)求办公楼AB的高度;
(2)若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.
(参考数据:sin22°≈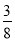 ,cos22°≈
,cos22°≈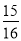 ,tan22°≈
,tan22°≈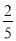 )
)
查看答案和解析>>
科目: 来源:内蒙古2017年中考数学二模试卷 题型:解答题
【问题情境】
已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
【数学模型】
设该矩形的长为x,周长为y,则y与x的函数表达式为y=2(x+ 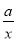 )(x>0).
)(x>0).
【探索研究】
小彬借鉴以前研究函数的经验,先探索函数y=x+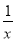 的图象性质.
的图象性质.
(1)结合问题情境,函数y=x+ 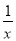 的自变量x的取值范围是x>0,下表是y与x的几组对应值.
的自变量x的取值范围是x>0,下表是y与x的几组对应值.

① 写出m的值;
②画出该函数图象,结合图象,得出当x=________时,y有最小值,y最小=________;
提示:在求二次函数y=ax2+bx+c(a≠0)的最大(小)值时,除了通过观察图象,还可以通过配方得到.试用配方法求函数y=x+ 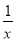 (x>0)的最小值,解决问题(2).
(x>0)的最小值,解决问题(2).
(2)【解决问题】
直接写出“问题情境”中问题的结论.
查看答案和解析>>
科目: 来源:内蒙古2017年中考数学二模试卷 题型:解答题
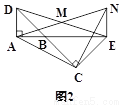
如图,△BAD和△BCE均为等腰直角三角形,∠BAD=∠BCE=90°,M为DE的中点.过点E作与AD平行的直线,交射线AM于点N.
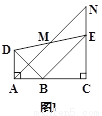
(1)当A,B,C三点在同一条直线上时(如图1),求证:M为AN中点.
(2)将图1中的△BCE绕点B旋转,当A,B,E三点在同一条直线上时(如图2),求证:△CAN为等腰直角三角形.
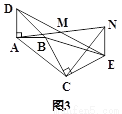
(3)将图1中的△BCE绕点B旋转到图3的位置时,(2)中的结论是否仍然成立?若成立,请证明;若不成立,请说明理由.
查看答案和解析>>
科目: 来源:内蒙古2017年中考数学二模试卷 题型:解答题
如图,抛物线y=ax2+bx+1经过点(2,6),且与直线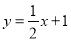 相交于A,B两点,点A在y轴上,过点B作BC⊥x轴,垂足为点C(4,0).
相交于A,B两点,点A在y轴上,过点B作BC⊥x轴,垂足为点C(4,0).
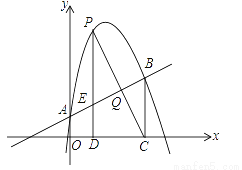
(1)求抛物线的解析式;
(2)若P是直线AB上方该抛物线上的一个动点,过点P作PD⊥x轴于点D,交AB于点E,求线段PE的最大值;
(3)在(2)的条件,设PC与AB相交于点Q,当线段PC与BE相互平分时,请求出点Q的坐标.
(1);(2)PE的最大值为4;(3)点Q的坐标为:(, ),(, ). 【解析】试题分析:(1)根据题意得出B点坐标,再利用待定系数法求出抛物线解析式; (2)首先表示出P,E点坐标,再利用PE=PD-ED,结合二次函数最值求法进而求出PE的最大值; (3)根据题意可得:PE=BC,则-x2+4x=3,进而求出Q点的横坐标,再利用直线上点的坐标性质得出答案. 试题解析:(...查看答案和解析>>
科目: 来源:2017-2018学年江苏省苏州市初二上期中试卷数学试卷 题型:单选题
在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目: 来源:2017-2018学年江苏省苏州市初二上期中试卷数学试卷 题型:单选题
下列各式中,正确的是( ).
A. 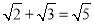 B.
B. 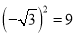 C.
C. 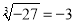 D.
D. 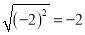
查看答案和解析>>
科目: 来源:2017-2018学年江苏省苏州市初二上期中试卷数学试卷 题型:单选题
平面直角坐标系内一点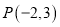 关于原点的对称点的坐标是( ).
关于原点的对称点的坐标是( ).
A. 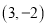 ? B.
? B. 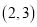 ? C.
? C. 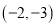 ? D.
? D. 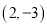
查看答案和解析>>
科目: 来源:2017-2018学年江苏省苏州市初二上期中试卷数学试卷 题型:单选题
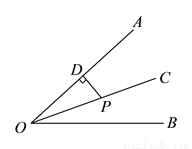
如图, 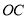 平分
平分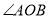 ,
, 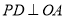 于点
于点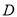 ,
, 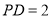 ,则
,则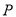 点到
点到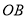 的距离是( ).
的距离是( ).
A.  B.
B. 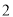 C.
C. 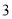 D.
D. 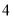
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com