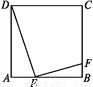
如图,E是正方形ABCD的边AB上的动点,EF⊥DE交BC于点F.

(1)求证:△ADE∽△BEF.

(2)设正方形的边长为4,AE=x,BF=y.当x取什么值时,y有最大值?并求出这个最大值.

（1）证明见解析；（2）1. 【解析】试题分析：（1）这两个三角形中，已知的条件有∠DAE=∠EBF=90°, 那么只要得出另外一组对应角相等即可得出两三角形相似，因为∠ADE+∠DEA=90°. 而∠AED+∠FEB=90°，因此∠ADE=∠FEB.那么就构成了两三角形相似的条件； （2）可用表示出BE的长，然后根据（1）中△ADE∽△BEF.可得出关于的比例关系式，然后就能...

如图(图①为实景侧视图,图②为安装示意图),在屋顶的斜坡面上安装太阳能热水器:先安装支架AB和CD(均与水平面垂直),再将集热板安装在AD上.为使集热板吸热率更高,公司规定:AD与水平线夹角为θ1,且在水平线上的射影AF为1.4 m.现已测量出屋顶斜面与水平面夹角为θ2,并已知tan θ1=1.082,tan θ2=0.412.如果安装工人已确定支架AB高为25 cm,求支架CD的高.(结果精确到1 cm)

119cm. 【解析】试题分析：过点A作AE∥BC,交CD于点E,作BG∥AF交DF的延长线于点G. 则∠EAF=θ2, EC=AB=25 cm.再根据锐角三角函数的定义用表示出的值，再根据进行解答即可． 试题解析：如图,过点A作AE∥BC,交CD于点E,作BG∥AF交DF的延长线于点G. 则∠EAF=∠CBG=θ2,且EC=AB=25 cm. 在Rt△DAF中,∠DAF=...

已知点A(-2,n)在抛物线y=x2+bx+c上.

(1)若b=1,c=3,求n的值;

(2)若此抛物线经过点B(4,n),且二次函数y=x2+bx+c的最小值是-4,请画出点P(x-1,x2+bx+c)的纵坐标随横坐标变化的图象,并说明理由.

(1)5;(2)作图见解析. 【解析】试题分析：（1）代入，以及点的坐标即可求得的值； （2）根据题意求得抛物线的解析式为从而求得点P(x-1,x2+bx+c)的纵坐标随横坐标变化的关系式为y=x'2-4,然后利用5点式画出函数的图象即可． 试题解析： (1) b=1,c=3,∴y=x2+x+3. 点A(-2,n)在抛物线y=x2+bx+c上, n=4-2+3=5....

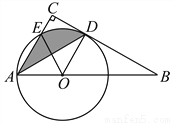
如图，点O为Rt△ABC斜边AB上的一点，以OA为半径的⊙O与BC切于点D，与AC交于点E，连接AD.

(1)求证：AD平分∠BAC；

(2)若∠BAC=60°，OA=2，求阴影部分的面积．(结果保留π)

（1）证明见解析；（2）S阴影＝π 【解析】试题分析：（1）由Rt△ABC中，∠C=90°，⊙O切BC于D，易证得AC∥OD，继而证得AD平分∠CAB． （2）如图，连接ED，根据（1）中AC∥OD和菱形的判定与性质得到四边形AEDO是菱形，则△AEM≌△DMO，则图中阴影部分的面积=扇形EOD的面积． 试题解析：（1）证明：∵⊙O切BC于D， ∴OD⊥BC， ∵AC...

△ABC是等边三角形,点A与点D的坐标分别是A(4,0),D(10,0).

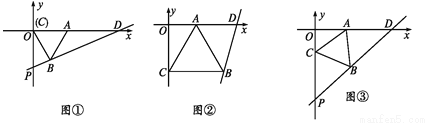
(1)如图①,当点C与点O重合时,求直线BD的表达式;

(2)如图②,点C从点O沿y轴向下移动,当以点B为圆心,AB为半径的☉B与y轴相切(切点为C)时,求点B的坐标;

(3)如图③,点C从点O沿y轴向下移动,当点C的坐标为C(0,-2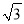)时,求∠ODB的正切值.

（1）y=x-.（2）点B的坐标为(8,-4).（3）. 【解析】试题分析：（1）先根据等边三角形的性质求出B点的坐标，直接运用待定系数法就可以求出直线BD的解析式。 （2）作BE⊥x轴于E，就可以得出∠AEB=90°，由圆的切线的性质就可以而出B的纵坐标，由直角三角形的性质就可以求出B点的横坐标，从而得出结论。 （3）以点B为圆心，AB为半径作⊙B，交y轴于点C、E，过点B作B...

如图，Rt△ABC中，∠C=90°，AB=7，∠B=35°，则AC的长为（ ）

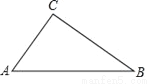
A. 7cos35° B. 7tan35° C. 7sin35° D. 7sin55°

C 【解析】∵在Rt△ABC中, ∠C=90°， ∴sin∠B=，即AC=AB sin∠B， ∵∠B=35°，AB=7， ∴AC=7sin35°. 故选：D.

若，则（ ）

A. B. C. D.

A 【解析】试题分析：∵ ∴ ∴ 故选A.

抛物线y=2(x+4)2-3的对称轴是 ( )

A. 直线x=4 B. 直线x=－4 C. 直线x=3 D. 直线x=－3

B 【解析】抛物线的顶点式方程为y=a（x-h）2+k，顶点坐标是（h，k），对称轴是x=h，所以抛物线y=2（x+4）2-3的对称轴是x=-4； 故选：B．

若△ABC的每条边长增加各自的10%得△A′B′C′，则∠B′的度数与其对应角∠B的度数相比（　　）

A. 增加了10% B. 减少了10% C. 增加了（1+10%） D. 没有改变

D 【解析】因为△ABC的每条边长增加各自的10%得△A′B′C′,所以△ABC和△A′B′C′的三条边对应成比例,所以△ABC∽△A′B′C′,所以∠B=∠B′,故选D.

如图，AB是⊙O的直径，C是⊙O上的一点，OD⊥BC于点D，AC=8，则OD的长为( )

A. 3 B. 4 C. 4.5 D. 5

B 【解析】∴CD=BD， ∵OA=OB，AC=8， ∴OD=AC=4. 故选：B.